题目内容
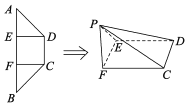
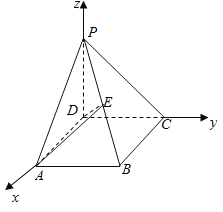
【题目】如图在棱锥
中，
为矩形，
面，
（1）在
上是否存在一点
，使
面
，若存在确定点位置，若不存在，请说明理由；
（2）当为中点时，求二面角
的余弦值.
【答案】（1）见解析；（2）
【解析】
（1）要证明PC⊥面ADE，由已知可得AD⊥PC，只需满足
即可，从而得到点E为中点;（2）求出面ADE的法向量，面PAE的法向量，利用空间向量的数量积，求解二面角P﹣AE﹣D的余弦值．
（1）法一：要证明PC⊥面ADE，易知AD⊥面PDC，即得AD⊥PC，故只需即可，
所以由
,即存在点E为PC中点.
法二：建立如图所示的空间直角坐标系D－XYZ， 由题意知PD＝CD＝1，
，设
， 
，
，由
，得
，
即存在点E为PC中点.
（2）由（1）知
，
，
，
，
， 
，
设面ADE的法向量为
，面PAE的法向量为
由的法向量为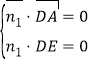
得，
得
，
同理求得
所以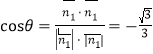
，
故所求二面角P－AE－D的余弦值为.
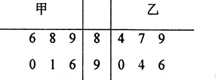
【题目】为了调查高中生的数学成绩与学生自主学习时间之间的相关关系，新苗中学数学教师对新入学的
名学生进行了跟踪调查，其中每周自主做数学题的时间不少于
小时的有
人，余下的人中，在高三模拟考试中数学成绩不足
分的占
，统计成绩后，得到如下的
列联表：
分数大于等于 | 分数不足 | 合计 | |
周做题时间不少于 | 4 | 19 | |
周做题时间不足 | |||
合计 | 45 |
（
）请完成上面的列联表，并判断能否在犯错误的概率不超过
的前提下认为“高中生的数学成绩与学生自主学习时间有关”．
（
）（i）按照分层抽样的方法，在上述样本中，从分数大于等于
分和分数不足分的两组学生中抽取
名学生，设抽到的不足分且周做题时间不足小时的人数为
，求的分布列（概率用组合数算式表示）．
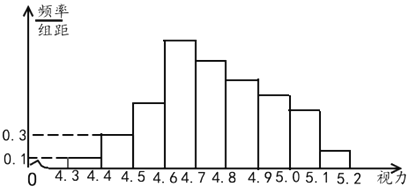
（ii）若将频率视为概率，从全校大于等于分的学生中随机抽取
人，求这些人中周做题时间不少于小时的人数的期望和方差．
附：
|
|
|
|
|
|
|
|
【题目】“新车嗨翻天!首付3000元起开新车”这就是毛豆新车网打出来的广告语．某人看到广告，兴奋不已，计划于2019年1月在该网站购买一辆某品牌汽车，他从当地了解到近五个月该品牌汽车实际销量如表：
月份 | 2018.08 | 2018.09 | 2018.10 | 2018.11 | 2018.12 |
月份编号t | 1 | 2 | 3 | 4 | 5 |
销量y（万辆） | 0.5 | 0.6 | 1 | 1.4 | 1.7 |
（1）经分析，可用线性回归模型拟合当地该品牌汽车实际销量y（万辆）与月份编号t之间的相关关系．请用最小二乘法求y关于t的线性回归方程
，并估计2019年1月份该品牌汽车的销量：
（2）为了增加销量，厂家和毛豆新车网联合推出对购该品牌车进行补贴．已知某地拟购买该品牌汽车的消费群体十分庞大，某调研机构对其中的200名消费者的购车补贴金额的心理预期值进行了一个抽样调查，得到如下一份频数表：
补贴金额预期值 区间（万元） | [1，2） | [2，3） | [3，4） | [4，5） | [5，6） | [6，7） |
频数 | 20 | 60 | 60 | 30 | 20 | 10 |
将频率视为概率，现用随机抽样方法从该地区拟购买该品牌汽车的所有消费者中随机抽取3人，记被抽取3人中对补贴金额的心理预期值不低于3万元的人数为ξ，求ξ的分布列及数学期望E（ξ）
参考公式及数据：①回归方程
，其中
，
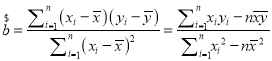；②
．