题目内容
设数列{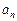 }的前n项和为
}的前n项和为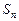 ,且
,且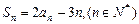 .
.
⑴证明数列{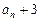 }为等比数列
}为等比数列
⑵求{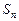 }的前n项和
}的前n项和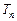
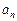 }的前n项和为
}的前n项和为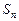 ,且
,且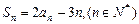 .
.⑴证明数列{
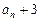 }为等比数列
}为等比数列⑵求{
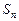 }的前n项和
}的前n项和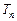
(1)见解析
(2)
(2)

⑴令n=1,S1=2a1-3. ∴a1 =3 由 Sn+1=2an+1-3(n+1), Sn=2an-3n,
两式相减,得 an+1 =2an+1-2an-3,
则 an+1=2an+3 .
 ,
, 所以{
所以{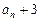 }为公比为2的等比数列
}为公比为2的等比数列
⑵an+3=(a1+3)·2n-1=6·2n-1,
∴an =6·2n-1-3


两式相减,得 an+1 =2an+1-2an-3,
则 an+1=2an+3 .
 ,
, 所以{
所以{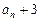 }为公比为2的等比数列
}为公比为2的等比数列⑵an+3=(a1+3)·2n-1=6·2n-1,
∴an =6·2n-1-3



练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 成等比数列, 公比为
成等比数列, 公比为 ,求证:
,求证: .
.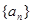 中,已知
中,已知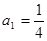 ,
,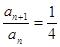 ,
,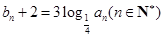 .
.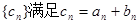 ,求
,求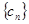 的前
的前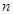 项和
项和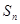 .
. 满足:
满足: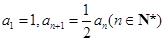 ,则
,则 _______ .
_______ . 的前
的前 项和为
项和为 ,且
,且 ,
, ,则
,则 ( )
( ) 中,
中, 则
则 ( )
( )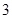

 或
或
 为等比数列,
为等比数列, ,
, ,则
,则 ( )
( )