题目内容
【题目】(2016·北京卷)如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥PD,PA=PD,AB⊥AD,AB=1,AD=2,AC=CD=![]() .
.
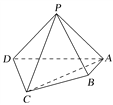
(1)求证:PD⊥平面PAB;
(2)求直线PB与平面PCD所成角的正弦值;
(3)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
【答案】(1) 见解析,(2)![]() ,(3)
,(3)![]()
【解析】试题分析:(1)先根据面面垂直性质定理得AB⊥平面PAD,即得AB⊥PD,再根据PA⊥PD,由线面垂直判定定理得结论, (2) 先根据条件建立空间直角坐标系,设立各点坐标,根据方程组解平面PCD法向量,根据向量数量积求向量夹角,最后根据线面角与向量夹角互余关系求直线PB与平面PCD所成角的正弦值;(3)由 BM∥平面PCD得向量BM与平面法向量垂直,根据向量数量积为零,解得![]() 的值.
的值.
试题解析: (1)证明 ∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,又AB⊥AD,AB平面ABCD,
∴AB⊥平面PAD.∵PD平面PAD.∴AB⊥PD.
又PA⊥PD,PA∩AB=A,
∴PD⊥平面PAB.

(2)解 取AD中点O,连接CO,PO,∵PA=PD,∴PO⊥AD.
又∵PO平面PAD,平面PAD⊥平面ABCD,
∴PO⊥平面ABCD.
∵CO平面ABCD,∴PO⊥CO.
∵AC=CD,∴CO⊥AD.
以O为原点建立如图所示空间直角坐标系.易知P(0,0,1),B(1,1,0),D(0,-1,0),C(2,0,0).
则![]() =(1,1,-1),
=(1,1,-1),![]() =(0,-1,-1),
=(0,-1,-1),![]() =(2,0,-1).
=(2,0,-1).
![]() =(-2,-1,0).
=(-2,-1,0).
设n=(x0,y0,1)为平面PDC的一个法向量.
由 得
得![]() 解得
解得
即n=![]() .
.
设PB与平面PCD的夹角为θ.
则sin θ=|cos〈n,![]() 〉|=
〉|= =
=
=![]() .
.
(3)解 设M是棱PA上一点,则存在λ∈[0,1]使得![]() =λ
=λ![]() ,因此点M(0,1-λ,λ),
,因此点M(0,1-λ,λ),![]() =(-1,-λ,λ).因为BM平面PCD,所以BM∥平面PCD,
=(-1,-λ,λ).因为BM平面PCD,所以BM∥平面PCD,
当且仅当![]() ·n=0,即(-1,-λ,λ)·
·n=0,即(-1,-λ,λ)·![]() =0,解得λ=
=0,解得λ=![]() ,所以在棱PA上存在点M使得BM∥平面PCD,此时
,所以在棱PA上存在点M使得BM∥平面PCD,此时![]() =
=![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】寒冷的冬天,某高中一组学生来到一大棚蔬菜基地,研究种子发芽与温度控制技术的关系,他们分别记录五组平均温度及种子的发芽数,得到如下数据:
平均温度 | 11 | 10 | 13 | 9 | 12 |
发芽数 | 25 | 23 | 30 | 16 | 26 |
(Ⅰ)若从五组数据中选取两组数据,求这两组数据平均温度相差不超过![]() 概率;
概率;
(Ⅱ)求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)若由线性回归方程得到的估计数据与实际数据的误差不超过2颗,则认为得到的线性回归方程是可靠的,试问(Ⅱ)屮所得的线性回归方程是否可靠?
(注:  ,
, ![]() )
)



