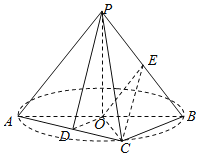
题目内容
【题目】如图所示,底面![]() 为菱形,
为菱形, ![]() ,
, ![]() ,
, ![]() 平面
平面![]() .
.

(1)设![]() 与
与![]() 交于点
交于点![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)求多面体![]() 的体积.
的体积.
【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析:(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,易证得四边形
,易证得四边形![]() 为平行四边形,所以
为平行四边形,所以![]() ,即可证得;
,即可证得;
(2)过点![]() 作
作![]() ,分别交^
,分别交^ ![]() 于点
于点![]() ,连接
,连接![]() ,
, ![]() .取
.取![]() 的中点
的中点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .由题意知,四边形
.由题意知,四边形![]() 为平行四边形,由
为平行四边形,由![]() ,结合
,结合![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,由体积公式求解即可.
,由体积公式求解即可.
试题解析:
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() .由题意知,
.由题意知, ![]() 为
为![]() 中点,∴
中点,∴![]() ,
,
又![]() ,∴
,∴![]() ,则四边形
,则四边形![]() 为平行四边形,
为平行四边形,
∴![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() ,分别交^
,分别交^ ![]() 于点
于点![]() ,连接
,连接![]() ,
, ![]() .取
.取![]() 的中点
的中点![]() ,连接
,连接![]() ,交
,交![]() 于点
于点![]() .由题意知,四边形
.由题意知,四边形![]() 为平行四边形.
为平行四边形.
∵![]() 为菱形,
为菱形, ![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() .
.
∵![]() 为等边三角形,
为等边三角形, ![]() 为
为![]() 的中点,∴
的中点,∴![]() ,
,
∵![]() 平面
平面![]() , ∴
, ∴![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() .
.
∵![]() 平面
平面![]() ,
, ![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() ,∴
,∴![]() .
.


练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
【题目】某校为了解高一实验班的数学成绩,采用抽样调查的方式,获取了![]() 位学生在第一学期末的数学成绩数据,样本统计结果如下表:
位学生在第一学期末的数学成绩数据,样本统计结果如下表:
分组 | 频数 | 频率 |
|
| |
|
| |
|
| |
|
| |
|
| |
|
| |
合计 |
|
|
(1)求![]() 的值和实验班数学平均分的估计值;
的值和实验班数学平均分的估计值;
(2)如果用分层抽样的方法从数学成绩小于![]() 分的学生中抽取
分的学生中抽取![]() 名学生,再从这
名学生,再从这![]() 名学生中选
名学生中选![]() 人,求至少有一个学生的数学成绩是在
人,求至少有一个学生的数学成绩是在![]() 的概率.
的概率.