题目内容
等差数列{an}的前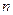 项和为Sn.已知S3=
项和为Sn.已知S3=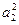 ,且S1,S2,S4成等比数列,则{an}的通项式为( )
,且S1,S2,S4成等比数列,则{an}的通项式为( )
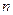 项和为Sn.已知S3=
项和为Sn.已知S3=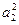 ,且S1,S2,S4成等比数列,则{an}的通项式为( )
,且S1,S2,S4成等比数列,则{an}的通项式为( )| A.2n |
| B.2n-1 |
| C.2n+1或3 |
| D.2n-1或3 |
D
∵S3=a1+a2+a3=3a2
∴3a2=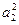
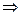 a2=0或 a2=3
a2=0或 a2=3
又S1,S2,S4成等比数列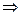 S22=S1·S4
S22=S1·S4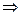 (2a2-d)2=(a2-d)(4a2+2d)
(2a2-d)2=(a2-d)(4a2+2d)
若a2=0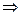 d2=-2d2
d2=-2d2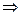 d=0,∴Sn=0,不合题意
d=0,∴Sn=0,不合题意
若a2=3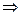 (6-d)2=(3-d)(12+2d)
(6-d)2=(3-d)(12+2d)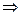 d=0或d=2
d=0或d=2
所以数列的通项公式为an=3或an=2n-1
∴3a2=
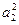
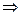 a2=0或 a2=3
a2=0或 a2=3又S1,S2,S4成等比数列
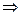 S22=S1·S4
S22=S1·S4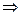 (2a2-d)2=(a2-d)(4a2+2d)
(2a2-d)2=(a2-d)(4a2+2d)若a2=0
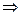 d2=-2d2
d2=-2d2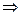 d=0,∴Sn=0,不合题意
d=0,∴Sn=0,不合题意若a2=3
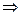 (6-d)2=(3-d)(12+2d)
(6-d)2=(3-d)(12+2d)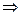 d=0或d=2
d=0或d=2所以数列的通项公式为an=3或an=2n-1

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
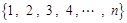
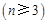 ,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为
,若该集合具有下列性质的子集:每个子集至少含有2个元素,且每个子集中任意两个元素之差的绝对值大于1,则称这些子集为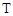 子集,记
子集,记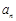 .
.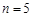 时,写出所有
时,写出所有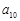 ;
;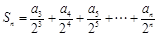 ,求证:
,求证: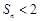
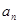 }的前n项和
}的前n项和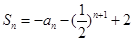 (n为正整数)。
(n为正整数)。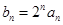 ,求证数列{
,求证数列{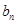 }是等差数列,并求数列{
}是等差数列,并求数列{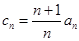 ,
,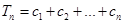 ,求
,求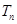 并证明:
并证明: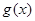 的前n项和为
的前n项和为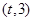 ,
,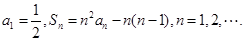
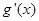 ;
;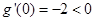 ,求证:
,求证: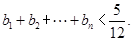
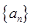 ,对任意的
,对任意的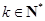 ,当
,当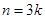 时,
时,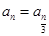 ;当
;当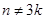 时,
时,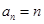 ,那么该数列中的第10个2是该数列的第 项.
,那么该数列中的第10个2是该数列的第 项.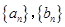 的前
的前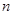 项和分别为
项和分别为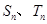 ,若
,若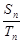 =
=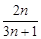 ,则
,则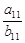 =_________
=_________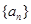 和
和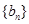 的前n项和分别为
的前n项和分别为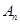 和
和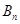 ,且
,且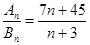 ,则使得
,则使得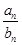 为整数的正整数n的个数是__________。
为整数的正整数n的个数是__________。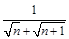 ,若前n项和为10,则项数n为( )
,若前n项和为10,则项数n为( )