题目内容
已知椭圆的中心在原点,焦点在x 轴上,离心率为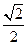 ,且椭圆经过圆C:
,且椭圆经过圆C: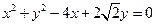 的圆心C。
的圆心C。
(1)求椭圆的方程;
(2)设直线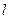 过椭圆的焦点且与圆C相切,求直线
过椭圆的焦点且与圆C相切,求直线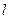 的方程。
的方程。
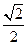 ,且椭圆经过圆C:
,且椭圆经过圆C: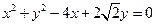 的圆心C。
的圆心C。(1)求椭圆的方程;
(2)设直线
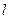 过椭圆的焦点且与圆C相切,求直线
过椭圆的焦点且与圆C相切,求直线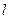 的方程。
的方程。(1)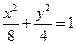
(2)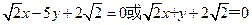
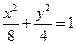
(2)
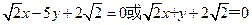
(1)圆C方程化为: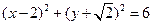 ,
,
圆心C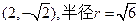 ………………………………………………………1分
………………………………………………………1分
设椭圆的方程为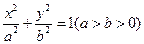 ,则……………………………………..2分
,则……………………………………..2分

所以所求的椭圆的方程是: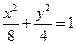 ………………………………………….6分
………………………………………….6分
(2)由(1)得到椭圆的左右焦点分别是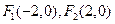 ,
,
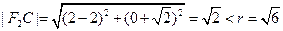
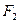 在C内,故过
在C内,故过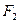 没有圆C的切线
没有圆C的切线
设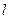 的方程为
的方程为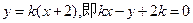 ……………………………………….8分
……………………………………….8分
点C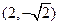 到直线
到直线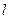 的距离为d
的距离为d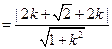 ,
,
由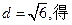
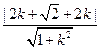 =
=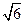 …………………………………………….9分
…………………………………………….9分
化简得: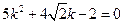
解得: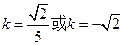 …………………………………………………………11分
…………………………………………………………11分
故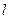 的方程为
的方程为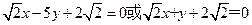 ……………………………12分
……………………………12分
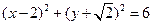 ,
,圆心C
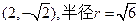 ………………………………………………………1分
………………………………………………………1分设椭圆的方程为
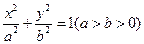 ,则……………………………………..2分
,则……………………………………..2分
所以所求的椭圆的方程是:
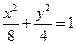 ………………………………………….6分
………………………………………….6分(2)由(1)得到椭圆的左右焦点分别是
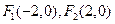 ,
,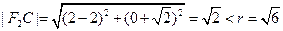
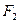 在C内,故过
在C内,故过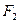 没有圆C的切线
没有圆C的切线设
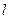 的方程为
的方程为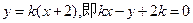 ……………………………………….8分
……………………………………….8分点C
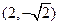 到直线
到直线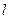 的距离为d
的距离为d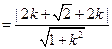 ,
,由
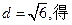
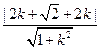 =
=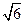 …………………………………………….9分
…………………………………………….9分化简得:
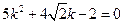
解得:
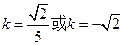 …………………………………………………………11分
…………………………………………………………11分故
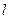 的方程为
的方程为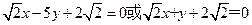 ……………………………12分
……………………………12分
练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
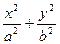 =1内有一个内接△ABC,它的一条边BC与长轴重合,A在椭圆上运动,试求△ABC重心的轨迹.
=1内有一个内接△ABC,它的一条边BC与长轴重合,A在椭圆上运动,试求△ABC重心的轨迹.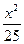 +
+ =1和椭圆C2:
=1和椭圆C2: +
+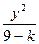 =1有( )
=1有( )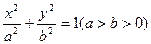
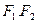
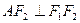
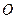
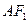
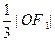
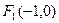 设过点
设过点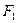 且不与坐标轴垂直的直线交椭圆于
且不与坐标轴垂直的直线交椭圆于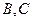 两点,线段
两点,线段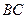 的垂直平分线与x轴交于
的垂直平分线与x轴交于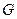 ,求点
,求点 与曲线C恒有公共点,求
与曲线C恒有公共点,求 的取值范围.
的取值范围.
 与椭圆
与椭圆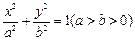 相交于
相交于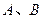 两点,且
两点,且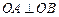 (其中
(其中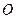 为坐标原点).(1)若椭圆的离心率为
为坐标原点).(1)若椭圆的离心率为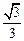 ,求椭圆的标准方程;
,求椭圆的标准方程;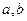 如何变化,椭圆恒过定点
如何变化,椭圆恒过定点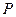
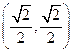 ;
;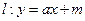 过(2)中的定点
过(2)中的定点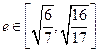 ,求原点到直线
,求原点到直线 距离的取值范围.
距离的取值范围.
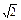 )且斜率为k的直线l与椭圆
)且斜率为k的直线l与椭圆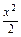 +y2=1有两个不同的交点P和Q.
+y2=1有两个不同的交点P和Q. +
+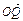 与
与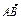 共线?如果存在,求k值;如果不存在,请说明理由.
共线?如果存在,求k值;如果不存在,请说明理由.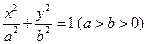 的面积为
的面积为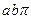 ,若全集
,若全集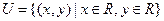 ,
,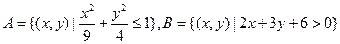 ,则
,则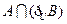 所表示的图形的面积为( ).
所表示的图形的面积为( ).

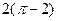
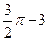
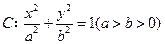 的左、右焦点分别是
的左、右焦点分别是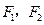 ,离心率为
,离心率为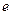 .直线
.直线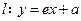 与
与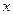 轴,
轴,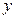 轴分别交于点
轴分别交于点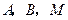 是直线
是直线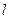 与椭圆
与椭圆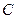 的一个公共点,
的一个公共点,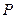 是点
是点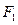 关于直线
关于直线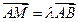 .
.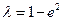 ;
;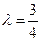 ,
,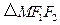 的周长为
的周长为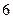 ,写出椭圆
,写出椭圆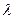 的值,使得
的值,使得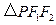 是等腰三角形.
是等腰三角形.