题目内容
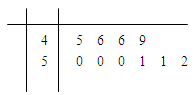
随机抽取某中学甲、乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如下图.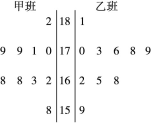
(1)根据茎叶图判断哪个班的平均身高较高;
(2)现从乙班这10名同学中随机抽取两名身高不低于173 cm的同学,求身高为176 cm的同学被抽中的概率.
(1)乙班平均身高高于甲班.(2) .
.
解析试题分析:(1)由茎叶图可知:甲班身高集中于160~179之间,而乙班身高集中于170~180之间,因此乙班平均身高高于甲班.…(6分)
(2)设身高为176 cm的同学被抽中的事件为A,
从乙班10名同学中抽中两名身高不低于173 cm的同学有:(181,173),(181,176),(181,178),(181,179),(179,173),(179,176),(179,178),(178,173),(178,176),(176,173)共10个基本事件,而事件A含有4个基本事件,∴P(A)= . (12分)
. (12分)
考点:本题考查了茎叶图的运用及古典概型的运用
点评:求古典概型事件的概率的步骤:(1)算出基本事件的总个数n;(2)算出随机事件A包含的基本事件数m;(3)依公式P(A)=算出事件A的概率.

 名校课堂系列答案
名校课堂系列答案某服装商场为了了解毛衣的月销售量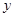 (件)与月平均气温
(件)与月平均气温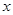 (℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
(℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:
月平均气温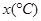 | 17 | 13 | 8 | 2 |
月销售量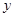 (件) (件) | 24 | 33 | 40 | 55 |
(2) 求线性回归方程
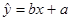 ;
;(3)气象部门预测下个月的平均气温约为6ºC,据此估计该商场下个月毛衣的销售量.(
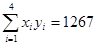 ,
,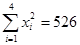 )
) 假设关于某设备使用年限x(年)和所支出的维修费用y(万元)有如下统计资料:若由资料知,y对x呈线性相关关系,试求:
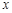 | 2 | 3 | 4 | 5 | 6 |
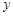 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
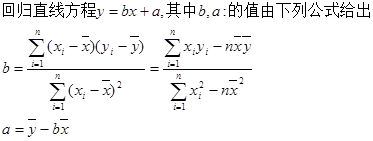 .
. 通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
性别与看营养说明列联表 单位: 名
| | 男 | 女 | 总计 |
| 看营养说明 | 50 | 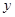 | 80 |
| 不看营养说明 |  | 20 | 30 |
| 总计 | 60 | 50 | 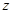 |
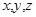 的值.
的值.(2)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
| 组号 | 分组 | 频数 | 频率 |
| 第一组 | [230,235) | 8 | 0.16 |
| 第二组 | [235,240) | ① | 0.24 |
| 第三组 | [240,245) | 15 | ② |
| 第四组 | [245,250) | 10 | 0.20 |
| 第五组 | [250,255] | 5 | 0.10 |
| 合 计 | 50 | 1.00 | |
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
在某次测验中,有6位同学的平均成绩为75分.用 表示编号为
表示编号为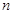
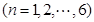 的同学所得成绩,且前5位同学的成绩如下:
的同学所得成绩,且前5位同学的成绩如下:
编号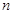 | 1 | 2 | 3 | 4 | 5 |
成绩 | 70 | 76 | 72 | 70 | 72 |
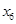 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差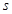 ;
;(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
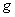 ,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位:
,为了了解这批食品的实际重量情况,从中随机抽取10袋食品,称出各袋的重量(单位: