题目内容
在某次测验中,有6位同学的平均成绩为75分.用 表示编号为
表示编号为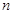
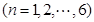 的同学所得成绩,且前5位同学的成绩如下:
的同学所得成绩,且前5位同学的成绩如下:
编号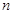 | 1 | 2 | 3 | 4 | 5 |
成绩 | 70 | 76 | 72 | 70 | 72 |
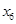 ,及这6位同学成绩的标准差
,及这6位同学成绩的标准差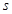 ;
;(2)从前5位同学中,随机地选2位同学,求恰有1位同学成绩在区间(68,75)中的概率.
(1)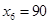
标准差
(2)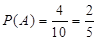
解析试题分析:(1)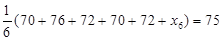 ,解得
,解得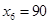
标准差
(2)前5位同学中随机选出的2位同学记为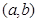 ,
,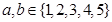 且
且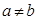
则基本事件有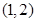 ,
,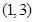 ,
,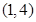 ,
,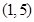 ,
,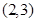 ,
,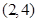 ,
,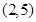 ,
, ,
,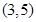 ,
,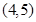 共10种
共10种
这5位同学中,编号为1、3、4、5号的同学成绩在区间(68,75)中
设A表示随机事件“从前5位同学中随机选出2位同学,恰有1位同学成绩在区间(68,75)中”
则A中的基本事件有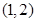 、
、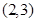 、
、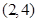 、
、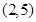 共4种,则
共4种,则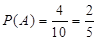
考点:本题主要考查样本标准差的意义及其计算,古典概型概率的计算。
点评:中档题,利用标准差计算公式,计算标准差,题目一般不难,数据较少,但仍需细心计算。古典概型概率的计算,关键是要弄清基本事件空间总数,事件的基本事件数。借助于“树图法”确保不重不漏。

练习册系列答案
相关题目
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
| 日 期 | 1月10日 | 2月10日 | 3月10日 | 4月10日 | 5月10日 | 6月10日 |
| 昼夜温差x(°C) | 10 | 11 | 13 | 12 | 8 | 6 |
| 就诊人数y(个) | 22 | 25 | 29 | 26 | 16 | 12 |
线性回归方程,再用被选取的2组数据进行检验.
(Ⅰ)求选取的2组数据恰好是相邻两个月的概率;
(Ⅱ)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x
的线性回归方程
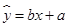 ;
; (Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2
人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理
想?
(参考公式:
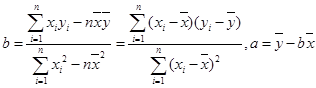 )
) 为了让学生了解更多“社会法律”知识,某中学举行了一次“社会法律知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
| 分组 | 频数 | 频率 |
| 60.5~70.5 | ① | 0.16 |
| 70.5~80.5 | 10 | ?② |
| 80.5~90.5 | 18 | 0.36 |
| 90.5~100.5 | ③ | ④ |
| 合计 | 50 | 1 |
(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为
000,001,002,…,799,试写出第二组第一位学生的编号 ;
(2)填充频率分布表的空格① ② ③ ④ 并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
调查某桑场采桑员和辅助工桑毛虫皮炎发病情况结果如下表:利用2×2列联表的独立性检验估计“患桑毛虫皮炎病与采桑”是否有关?认为两者有关系会犯错误的概率是多少?
| | 采桑 | 不采桑 | 合计 |
| 患者人数 | 18 | 12 | |
| 健康人数 | 5 | 78 | |
| 合计 | | | |
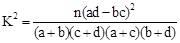
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
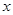 与销售额
与销售额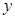 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据: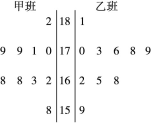
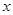 与销售额
与销售额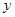 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据: .
.