题目内容
通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:
性别与看营养说明列联表 单位: 名
| | 男 | 女 | 总计 |
| 看营养说明 | 50 | 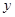 | 80 |
| 不看营养说明 |  | 20 | 30 |
| 总计 | 60 | 50 | 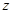 |
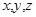 的值.
的值.(2)根据以上列联表,问有多大把握认为“性别与在购买食物时看营养说明”有关?
(1)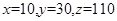
(2)有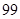 %的把握认为该校高中学生“性别与在购买食物时看营养说明”有关.
%的把握认为该校高中学生“性别与在购买食物时看营养说明”有关.
解析试题分析:(1)根据列联表可以得出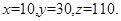 3分
3分
(2)假设 :该校高中学生性别与在购买食物时看营养说明无关,则
:该校高中学生性别与在购买食物时看营养说明无关,则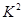 应该很小. 5分
应该很小. 5分
根据题中的列联表得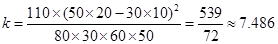 8分
8分
由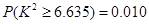 , 10分
, 10分
有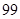 %的把握认为该校高中学生“性别与在购买食物时看营养说明”有关. 12分
%的把握认为该校高中学生“性别与在购买食物时看营养说明”有关. 12分
考点:本小题主要考查列联表和独立性检验.
点评:解决独立性检验问题时,要注意步骤和最后回答时的准确性。

练习册系列答案
相关题目
为考查某种药物预防疾病的效果,进行动物试验,得到如下丢失数据的列联表:
药物效果试验列联表
| | 患病 | 未患病 | 总计 |
| 没服用药 | 20 | 30 | 50 |
| 服用药 | x | y | 50 |
| 总计 | M | N | 100 |
 P(Y=0).
P(Y=0).(1)求出列联表中数据x,y,M,N的值;
(2)能够有多大的把握认为药物有效?
(3)现在从该100头动物中,采用随机抽样方法每次抽取1头,抽后返回,抽取5次, 若每次抽取的结果是相互独立的,记被抽取的5头中为服了药还患病的数量为
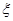 .,求
.,求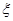 的期望E(
的期望E(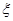 )和方差D(
)和方差D(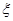 ).
).参考公式:
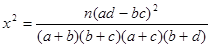 (其中
(其中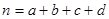 )
)| P(K2≥k) | 0.25 | 0.15 | 0.10 | 0.05 | 0.010 | 0.005 |
| k | 1.323 | 2.072 | 2.706 | 3.845 | 6.635 | 7.879 |
近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机的对入院50人进行了问卷调查得到了如下的列联表:
| | 患心肺疾病 | 不患心肺疾病 | 合计 |
| 男 | | 5 | |
| 女 | 10 | | |
| 合计 | | | 50 |
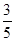 .
.(Ⅰ)请将上面的列联表补充完整;
(Ⅱ)是否有
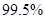 的把握认为患心肺疾病与性别有关?说明你的理由;
的把握认为患心肺疾病与性别有关?说明你的理由;(Ⅲ)已知在患心肺疾病的10位女性中,有3位又患胃病.现在从患心肺疾病的10位女性中,选出3名进行其他方面的排查,记选出患胃病的女性人数为
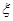 ,求
,求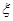 的分布列,数学期望以及方差.
的分布列,数学期望以及方差.下面的临界值表供参考:
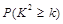 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
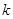 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
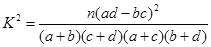 其中
其中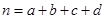 )
) 为了让学生了解更多“社会法律”知识,某中学举行了一次“社会法律知识竞赛”,共有800名学生参加了这次竞赛. 为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
| 分组 | 频数 | 频率 |
| 60.5~70.5 | ① | 0.16 |
| 70.5~80.5 | 10 | ?② |
| 80.5~90.5 | 18 | 0.36 |
| 90.5~100.5 | ③ | ④ |
| 合计 | 50 | 1 |
(1)若用系统抽样的方法抽取50个样本,现将所有学生随机地编号为
000,001,002,…,799,试写出第二组第一位学生的编号 ;
(2)填充频率分布表的空格① ② ③ ④ 并作出频率分布直方图;
(3)若成绩在85.5~95.5分的学生为二等奖,问参赛学生中获得二等奖的学生约为多少人?
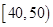 ,
,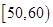 ,
,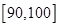 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.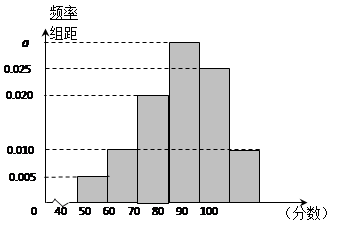
 的值;
的值;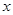 与销售额
与销售额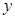 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据: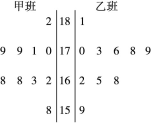
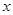 与销售额
与销售额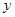 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据: