题目内容
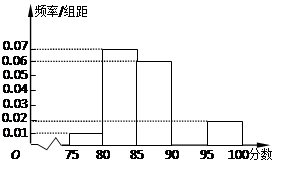
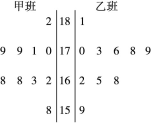
我校某班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如下,据此解答如下问题.
(1)求全班人数及分数在[80,90)之间的频数;
(2)估计该班的平均分数,并计算频率分布直方图中[80,90)间的矩形的高;
(3)若要从分数在[80,100]之间的试卷中任取两份分析学生失分情况,在抽取的试卷中,求至少有一份分数在[90,100]之间的概率.
(1)分数在[80,90)之间的频数为25-2-7-10-2=4;
(2)频率分布直方图中[80,90)间的矩形的高为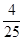 ÷10=0.016;
÷10=0.016;
(3)至少有一份分数在[90,100]之间的概率是 =0.6
=0.6
解析试题分析:(1)由茎叶图知,分数在[50,60)之间的频数为2,
频率为0.008×10=0.08 全班人数 ="25"
="25"
所以分数在[80,90)之间的频数为25-2-7-10-2=4…………3分
(2)分数在[50,60)之间的总分数为56+58=114
分数在[60,70)之间的总分数为60×7+2+3+3+5+6+8+9=456
分数在[70,80)之间的总分数为70×10+1+2+2+3+4+5+6+7+8+9=747
分数在[80,90)之间的总分数为85×4=340分数在[90,100]之间的总分数为95+98=193
所以,该班的平均分数为 ……………5分
……………5分
估计平均分数时,以下解法也给分:
分数在[50,60)之间的频率为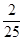 =0.08分数在[60,70)之间的频率为
=0.08分数在[60,70)之间的频率为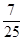 =0.28
=0.28
分数在[70,80)之间的频率为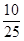 =0.40分数在[80,90)之间的频率为
=0.40分数在[80,90)之间的频率为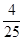 =0.16
=0.16
分数在[90,100]之间的频率为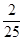 =0.08所以该班的平均分数约为55×0.08+65×0.28+75×0.40+85×0.16+95×0.08 =73.8
=0.08所以该班的平均分数约为55×0.08+65×0.28+75×0.40+85×0.16+95×0.08 =73.8
所以频率分布直方图中[80,90)间的矩形的高为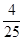 ÷10=0.016………………8分
÷10=0.016………………8分
(3)将[80,90)之间的4个分数编号为1,2,3,4,[90,100]之间的2个分数编号为5,6,
在[80,100]之间的试卷中任取两份的基本事件为(1,2),(1,3),(1,4),(1,5)(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6),共15个.
其中,至少有一份在[90,100]之间的基本事件有9个,故至少有一份分数在[90,100]之间的概率是 =0.6…
=0.6…
考点:本题主要考查茎叶图,频率的概念及计算,古典概型概率的计算。
点评:典型题,统计中的抽样方法,频率直方图,概率计算及分布列问题,是高考必考内容及题型。古典概型概率的计算问题,关键是明确基本事件数,往往借助于“树图法”,做到不重不漏。频率分布直方图中,小矩形的高等于每一组的频率÷组距,它们与频数成正比,小矩形的面积等于这一组的频率,则组距等于频率除以高。

 步步高达标卷系列答案
步步高达标卷系列答案为了解目前老年人居家养老还是在敬老院养老的意向,共调查了50名老年人,其中男性明确表示去敬老院养老的有5人,女性明确表示居家养老的有10人,已知在全部50人中随机地抽取1人明确表示居家养老的概率为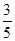 。
。
(1)请根据上述数据建立一个2×2列联表;
(2)居家养老是否与性别有关?请说明理由。
参考公式: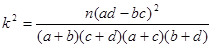
参考数据:
 | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
调查某桑场采桑员和辅助工桑毛虫皮炎发病情况结果如下表:利用2×2列联表的独立性检验估计“患桑毛虫皮炎病与采桑”是否有关?认为两者有关系会犯错误的概率是多少?
| | 采桑 | 不采桑 | 合计 |
| 患者人数 | 18 | 12 | |
| 健康人数 | 5 | 78 | |
| 合计 | | | |
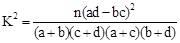
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
(本题满分12分)
某车间为了规定工时定额,需要确定加共某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2)试预测加工10个零件需要多少时间?
 与销售额
与销售额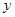 (单位:百万元)之间有如下对应数据:
(单位:百万元)之间有如下对应数据: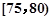 ,第2组
,第2组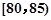 ,第3组
,第3组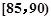 ,第4组
,第4组 ,第5组
,第5组 ,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
,得到的频率分布直方图如图所示,同时规定成绩在85分以上(含85分)的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.