题目内容
【题目】已知公差不为零的等差数列{an}中,a1=1且a1 , a3 , a9成等比数列, (Ⅰ)求数列{an}的通项公式
(Ⅱ)设bn=n2 ![]() 求数列[bn}的前n项和Sn .
求数列[bn}的前n项和Sn .
【答案】解:(Ⅰ)设数列{an}的公差为d≠0. ∵a1=1,且a1 , a3 , a9成等比数列,
∴a32=a1a9 , 即(1+2d)2=1×(1+8d),
∴4d2=8d,∵d≠0,∴d=1.
∴an=a1+(n﹣1)=1+n﹣1=n.
(Ⅱ)∵bn=n2 ![]() =n2n
=n2n
∴Sn=121+222+323+…+(n﹣1)2n﹣1+n2n…①
2Sn=122+223+…+(n﹣2)2n﹣1+(n﹣1)2n+n2n+1…②
①﹣②得﹣Sn=2+22+23+…+2n﹣n2n﹣1=2n+1(1﹣n)﹣2.
∴Sn=(n﹣1)2n+1+2.
【解析】(Ⅰ)设数列{an}的公差为d≠0.由a1=1,且a1 , a3 , a9成等比数列,可得a32=a1a9 , 即(1+2d)2=1×(1+8d),解出d即可得出通项公式;(Ⅱ)bn=n2 ![]() =n2n , 利用错位相减法求和即可.
=n2n , 利用错位相减法求和即可.
【考点精析】认真审题,首先需要了解数列的前n项和(数列{an}的前n项和sn与通项an的关系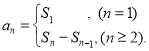 ),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.
),还要掌握数列的通项公式(如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式)的相关知识才是答题的关键.

 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案【题目】某社区为丰富居民节日活动,组织了“迎新春”象棋大赛,已知报名的选手情况统计如下表:
组别 | 男 | 女 | 总计 |
中年组 |
|
| 91 |
老年组 | 16 |
|
|
已知中年组女性选手人数是仅比老年组女性选手人数多2人,若对中年组和老年组分别利用分层抽样的方法抽取部分报名者参加比赛,已知老年组抽取了5人,其中女性3人,中年组抽取了7人.
(1)求表格中的数据![]() ;
;
(2)若从选出的中年组的选手中随机抽取两名进行比赛,求至少有一名女性选手的概率.