题目内容
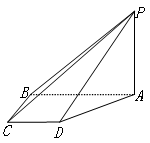
如图,在四棱锥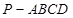 中,
中,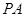 ⊥底面
⊥底面 ,四边形
,四边形 是直角梯形,
是直角梯形,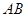 ⊥
⊥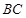 ,
,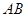 ∥
∥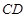 ,
,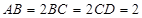 ,
,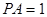 .
.
(1)求证:平面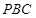 ⊥平面
⊥平面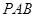 ;
;
(2)求点C到平面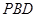 的距离;
的距离;
(3)求PC与平面PAD所成的角的正弦值。
(1)见解析;(2)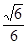 ;(3)
;(3)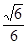 。
。
解析试题分析:(1) 平面
平面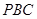 ,需证BC⊥平面PAB, 由
,需证BC⊥平面PAB, 由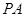 ⊥底面
⊥底面 得PA⊥BC,又已知
得PA⊥BC,又已知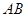 ⊥
⊥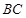 ,
,
故问题得证;(2)利用等体积转化法,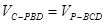 ;(3)根据线面角的定义,求出点C到平面PAD的距离、线段
;(3)根据线面角的定义,求出点C到平面PAD的距离、线段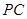 的长度,即可求出PC与平面PAD所成的角的正弦值。
的长度,即可求出PC与平面PAD所成的角的正弦值。
试题解析:(1)∵PA⊥平面ABCD, BC Ì平面ABCD,∴PA⊥BC,
又AB⊥BC,PA∩AB=A, ∴BC⊥平面PAB,
∵BC Ì平面PBC, ∴平面PBC⊥平面PAB
(2)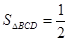 , ∵
, ∵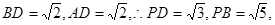
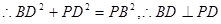 ,
,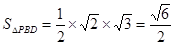
设点C到平面PBD的距离为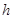 ,∵
,∵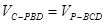 ,
,
∴ ,∴
,∴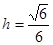
由(2)知, 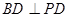 ,又
,又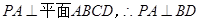 ,∴
,∴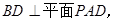 连接AC交BD于E,
连接AC交BD于E,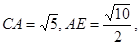
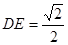 ,
,
由相似形可得,点C到平面PAD的距离=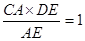 ,
,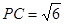 ,
,
∴PC与平面PAD所成的角的正弦值是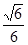 。
。
考点:(1)空间线面平垂直、面面平垂直判定定理的应用;(2)空间线面角的定义及求法;(3)空间点面距离概念与求法。

练习册系列答案
相关题目
 中,
中,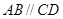 ,
,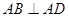 ,且
,且 .现以
.现以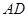 为一边向形外作正方形
为一边向形外作正方形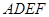 ,然后沿边
,然后沿边 为
为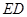 的中点,如图2.
的中点,如图2.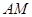 ∥平面
∥平面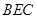 ;
;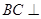 平面
平面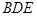 ;
; 到平面
到平面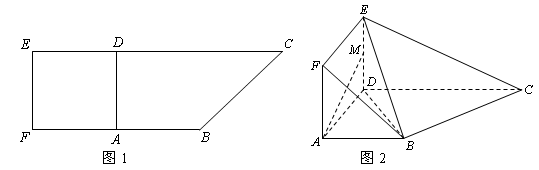
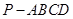 的底面为直角梯形,
的底面为直角梯形, ,
,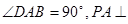 底面
底面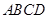 ,且
,且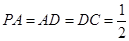 ,
,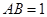 ,
,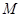 是
是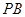 的中点.
的中点.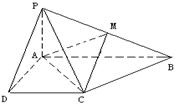
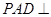 面
面 ;
;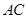 与
与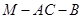 的正弦值.
的正弦值. 中,
中, 、
、 分别为
分别为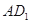 ,
, 中点。
中点。 与
与 所成角的大小;
所成角的大小; 平面
平面 。
。
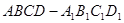 中,已知平面
中,已知平面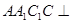 平面
平面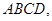 且
且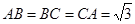 ,
,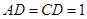 .
.
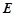 为棱
为棱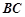 上的一点,且
上的一点,且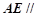 平面
平面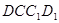 ,求线段
,求线段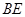 的长度
的长度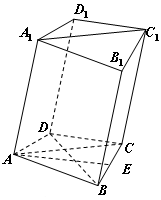

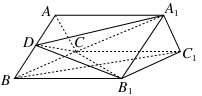
 的侧棱与底面垂直,且
的侧棱与底面垂直,且 ,
,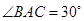 ,
, ,
, ,点
,点 、
、 、
、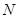 分别为
分别为 、
、 、
、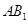 的中点.
的中点. 平面
平面 ;
; ;
; 的余弦值.
的余弦值.
 a,则它的5个面中,互相垂直的面有 对.
a,则它的5个面中,互相垂直的面有 对.