题目内容
【题目】如图,四棱锥![]() 的底面
的底面![]() 为直角梯形,
为直角梯形,![]() ,且
,且![]()
![]() 为等边三角形,平面
为等边三角形,平面![]() 平面
平面![]() ;点
;点![]() 分别为
分别为![]() 的中点.
的中点.

(1)证明:![]() 平面
平面![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)求解线面平行,根据题意,连接相应的中位线,根据中位线的关系可得,四边形![]() 是平行四边形.
是平行四边形.
(2) 设![]() 的中点为
的中点为![]() , 可证
, 可证![]() 两两垂直,以点
两两垂直,以点![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立坐标系,然后求出平面
轴建立坐标系,然后求出平面![]() 的法向量,最后利用向量的内积关系即可求解出直线
的法向量,最后利用向量的内积关系即可求解出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,
![]() 为
为![]() 的中点,所以
的中点,所以![]() 为
为![]() 的中位线,
的中位线,
则可得![]() ,且
,且![]() ;
;
在梯形![]() 中,
中,![]() ,且
,且![]() ,
,
![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
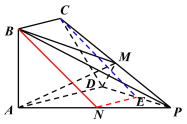
法二:设![]() 为
为![]() 的中点,连接
的中点,连接![]() ,
,
![]() 为
为![]() 的中点,
的中点,
所以![]() 是
是![]() 的中位线,所以
的中位线,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又在梯形![]() 中,
中,![]() ,且
,且![]() ,
,
所以四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又![]() ,
,
所以平面![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
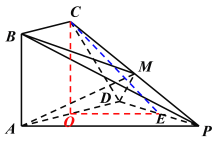
(2)设![]() 的中点为
的中点为![]() ,又
,又![]() .
.
因为平面![]() 平面
平面![]() ,交线为
,交线为![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,
又由![]() ,
,![]() ,
,
![]() .
.
即有![]() 两两垂直,如图,以点
两两垂直,如图,以点![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立坐标系.
轴建立坐标系.
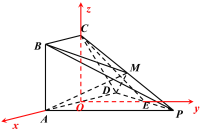
已知点![]() ,
,
设平面![]() 的法向量为:
的法向量为:![]() .
.
则有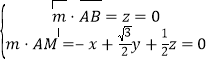 ,可得平面
,可得平面![]() 的一个法向量为
的一个法向量为![]() ,
,
![]() ,
,
可得: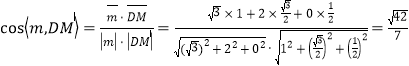 ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

练习册系列答案
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案
相关题目
【题目】某高校“统计”课程的教师随机调查了选该课的一些学生的情况,具体数据如下表,为了判断主修统计专业是否与性别有关,计算得到![]() ,因为
,因为![]() ,所以判定主修统计专业与性别是有关系的,那么这种判断出错的可能性为________.
,所以判定主修统计专业与性别是有关系的,那么这种判断出错的可能性为________.
专业 性别 | 非统计专业 | 统计专业 |
男 | 13 | 10 |
女 | 7 | 20 |
本题可以参考独立性检验临界值表:
| 0.5 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

