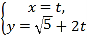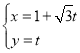题目内容
【题目】由甲乙两位同学组成一个小组参加年级组织的篮球投篮比赛，共进行两轮投篮，每轮甲乙各自独立投篮一次，并且相互不受影响，每次投中得2分，没投中得0分.已知甲同学每次投中的概率为
，乙同学每次投中的概率为
（1）求第一轮投篮时，甲乙两位同学中至少有一人投中的概率；
（2）甲乙两位同学在两轮投篮中，记总得分为随机变量ξ，求ξ的分布列和期望.
【答案】（1）
（2）详见解析
【解析】
（1）利用相互独立事件的概率乘法公式求出都没有投中的概率，从而可求出至少有一人投中的概率.
（2）根据题意可得随机变量ξ
，首先利用独立重复试验的概率乘法公式求出甲乙各得分的概率，从而可得总得分为随机变量ξ分布列，进而可得数学期望.
解：（1）第一轮投篮时，甲乙两位同学中都没有投中的概率为
甲乙两位同学中至少有一人投中的概率为
.
（2）对甲：
，
，
对乙：
，
，
，
Y=0 | Y=2 | Y=4 | P(X=j) | |
X=0 |
|
|
|
|
X=2 |
|
|
|
|
X=4 |
|
|
|
|
P(Y=i) |
|
|
|
记
：则有
，
，
，
，
，
所以，
练习册系列答案
相关题目
