ƒøƒĞ»ı
°æƒø°øŒ™¡À÷Œ¿Ìø’∆¯Œğ»æ£¨ƒ≥ –…Ë9∏ˆº‡≤‚’æ”√”к‡≤‚ø’∆¯÷ ¡ø÷∏ ˝£®AQI£©£¨∆‰÷–‘Ğ«·∂»Œğ»æ«¯°¢÷–∂»Œğ»æ«¯°¢÷ÿ∂»Œğ»æ«¯∑÷±…Ë”–2°¢4°¢3∏ˆº‡≤‚’棨≤¢“‘9∏ˆº‡≤‚’æ≤‚µ√µƒAQIµƒ∆Ωæ˘÷µŒ™“¿æı≤•±®∏√ –µƒø’∆¯÷ ¡ø.
£®1£©»Ùƒ≥»’≤•±®µƒAQIŒ™119£¨“—÷™«·∂»Œğ»æ«¯AQI∆Ωæ˘÷µŒ™70£¨÷–∂»Œğ»æ«¯AQI∆Ωæ˘÷µŒ™115£¨«Û÷ÿ ‘Œğ»æ«¯AQI∆Ωæ˘÷µ£ª
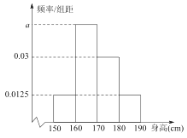
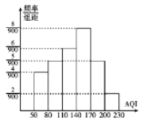
£®2£©»ÁÕº «2018ƒÍ11‘¬∑ı30ÃϵƒAQIµƒ∆µ¬ ∑÷≤º÷±∑ΩÕº£¨11‘¬∑ıΩˆ”–1ÃÏAQI‘Ğ![]() ƒĞ.
ƒĞ.
¢Ÿƒ≥–£≤Œ’’πŸ∑Ωπ´≤ºµƒAQI£¨»Áπ˚÷İ»’AQI–°”Ğ150æÕ◊È÷Ø—ß…˙≤Œº”ªßÕ‚ªÓ∂Ø£¨“‘Õ≥º∆ ˝æı÷–µƒ∆µ¬ Œ™∏≈¬ £¨«Û∏√–£—ß…˙÷İ»’ƒİ≤Œº”ªßÕ‚ªÓ∂صƒ∏≈¬ £ª
¢Ğª∑Œ¿≤ø√≈¥”11‘¬∑ıAQI≤ª–°”Ğ170µƒ ˝æı÷–≥È»°»˝Ãϵƒ ˝æıΩ¯––—–æø£¨«Û≥È»°µƒ’‚»˝ÃÏ÷–AQI÷µ≤ª–°”Ğ200µƒÃÏ ˝µƒ∑÷≤º¡–∫Õ ˝—ß∆ĞÕ˚.
°æ¥∞∏°ø£®1£©![]() £®2£©¢Ÿ
£®2£©¢Ÿ![]() ¢ĞœÍº˚Ω‚Œˆ
¢ĞœÍº˚Ω‚Œˆ
°æΩ‚Œˆ°ø
£®1£©…Ë÷ÿ∂»Œğ»æ«¯AQI∆Ωæ˘÷µŒ™![]() ,∏˘æı√ø»’9∏ˆº‡≤‚’æ≤‚µ√µƒAQI◊İ÷µΩ¯––«ÛΩ‚º¥ø…£ª
,∏˘æı√ø»’9∏ˆº‡≤‚’æ≤‚µ√µƒAQI◊İ÷µΩ¯––«ÛΩ‚º¥ø…£ª
£®2£©¢Ÿ”…∆µ¬ ∑÷≤º÷±∑ΩÕºø…µ√AQI‘Ğ≤ª–°”Ğ140µƒ≤ªÕ¨«¯º‰µƒ∆µ ˝,‘Ÿ∏˘æı11‘¬∑ıΩˆ”–1ÃÏAQI‘Ğ![]() ƒĞ,º¥ø…ªÒµ√AQI≤ª–°”Ğ150µƒ∆µ ˝,Ω¯∂¯«ÛΩ‚£ª
ƒĞ,º¥ø…ªÒµ√AQI≤ª–°”Ğ150µƒ∆µ ˝,Ω¯∂¯«ÛΩ‚£ª
¢Ğ”…¢Ÿ, AQI≤ª–°”Ğ170Ãϵƒπ≤7ÃÏ,≤ª–°”Ğ200Ãϵƒπ≤2ÃÏ,‘Ú![]() µƒÀ˘”–ø…ƒİ»°÷µŒ™0,1,2,
µƒÀ˘”–ø…ƒİ»°÷µŒ™0,1,2,
Ω¯∂¯∏˘æı≥¨º∏∫Œ∑÷≤º«ÛΩ‚∑÷≤º¡–∫Õ∆ĞÕ˚.
Ω‚:£®1£©…Ë÷ÿ∂»Œğ»æ«¯AQI∆Ωæ˘÷µŒ™![]() ,
,
‘Ú![]() ,Ω‚µ√
,Ω‚µ√![]() .
.
£®2£©¢ŸAQI‘Ğ![]() …œµƒ”–
…œµƒ”–![]() ÃÏ,
ÃÏ,
AQI‘Ğ![]() …œµƒ”–
…œµƒ”–![]() ÃÏ,
ÃÏ,
AQI‘Ğ![]() …œµƒ”–
…œµƒ”–![]() ÃÏ,
ÃÏ,
“ÚŒ™11‘¬∑ıΩˆ”–1ÃÏAQI‘Ğ![]() ƒĞ,
ƒĞ,
À˘“‘11‘¬∑ıAQI≤ª–°”Ğ150µƒπ≤![]() ÃÏ,
ÃÏ,
º¥ƒİ≤Œº”ªßÕ‚ªÓ∂صƒ∏≈¬ Œ™![]() .
.
¢Ğ”…¢Ÿ,AQI≤ª–°”Ğ170Ãϵƒπ≤7ÃÏ,≤ª–°”Ğ200Ãϵƒπ≤2ÃÏ,
‘Ú![]() µƒÀ˘”–ø…ƒİ»°÷µŒ™0,1,2,
µƒÀ˘”–ø…ƒİ»°÷µŒ™0,1,2,
À˘“‘![]() ,
,![]() ,
,![]() ,
,
À˘“‘![]() µƒ∑÷≤º¡–Œ™:
µƒ∑÷≤º¡–Œ™:
| 0 | 1 | 2 |
|
|
|
|
‘Ú![]() .
.

 ÃÏÃϜڅœøŒ ±Õ¨≤Ω—µ¡∑œµ¡–¥∞∏
ÃÏÃϜڅœøŒ ±Õ¨≤Ω—µ¡∑œµ¡–¥∞∏ —Ùπ‚øŒÃ√Õ¨≤Ω¡∑œ∞œµ¡–¥∞∏
—Ùπ‚øŒÃ√Õ¨≤Ω¡∑œ∞œµ¡–¥∞∏