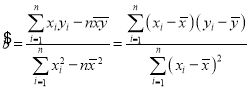题目内容
【题目】FEV1(一秒用力呼气容积)是肺功能的一个重要指标.为了研究某地区10~15岁男孩群体的FEV1与身高的关系,现从该地区A、B、C三个社区10~15岁男孩中随机抽取600名进行FEV1与身高数据的相关分析.
(1)若A、B、C三个社区10~15岁男孩人数比例为1:3:2,按分层抽样进行抽取,请求出三个社区应抽取的男孩人数.
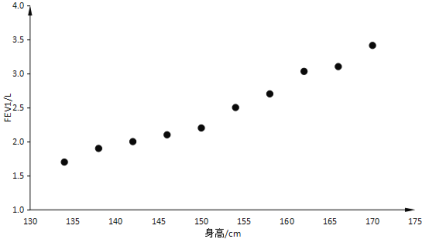
(2)经过数据处理后,得到该地区10~15岁男孩身高![]() (cm)与FEV1
(cm)与FEV1![]() (L)对应的10组数据
(L)对应的10组数据![]() ,并作出如下散点图:
,并作出如下散点图:
经计算得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 的相关系数
的相关系数![]() .
.
①请你利用所给公式与数据建立![]() 关于
关于![]() 的线性回归方程,并估计身高160cm的男孩的FEV1的预报值
的线性回归方程,并估计身高160cm的男孩的FEV1的预报值![]() .
.
②已知若①中回归模型误差的标准差为![]() ,则该地区身高160cm的男孩的FEV1的实际值落在
,则该地区身高160cm的男孩的FEV1的实际值落在![]() ,
,![]() 内的概率为
内的概率为![]() .现已求得
.现已求得![]() ,若该地区有两个身高160cm的12岁男孩M和N,分别测得FEV1值为2.8L和2.3L,请结合概率统计知识对两个男孩的FEV1指标作出一个合理的推断与建议.
,若该地区有两个身高160cm的12岁男孩M和N,分别测得FEV1值为2.8L和2.3L,请结合概率统计知识对两个男孩的FEV1指标作出一个合理的推断与建议.
附:样本![]() 的相关系数
的相关系数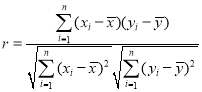 ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为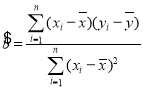 ,
,![]() ,
,![]() .
.
【答案】(1)100;300;200;(2)①![]() .2.84;②见解析
.2.84;②见解析
【解析】
(1)根据抽样比分别为![]() ,即可得答案;
,即可得答案;
(2)①根据最小二乘法公式,可求得线性回归方程![]() ;再利用回归方程可求得预报值;
;再利用回归方程可求得预报值;
②由题意可知,该地区身高![]() 的男孩的
的男孩的![]() 的实际值落在区间
的实际值落在区间![]() 内的概率为99.74%,即该地区身高
内的概率为99.74%,即该地区身高![]() 的男孩的
的男孩的![]() 值不在这个区间内的概率极小,仅有0.26%,
值不在这个区间内的概率极小,仅有0.26%,![]() 的
的![]() 值落在该区间内,可推断他的
值落在该区间内,可推断他的![]() 值是正常的;
值是正常的;
(1)![]() 社区抽取人数:
社区抽取人数:![]() ;
;![]() 社区抽取人数:
社区抽取人数:![]() ;
;![]() 社区抽取人数:
社区抽取人数:![]() .
.
(2)①对比![]() 公式,可得
公式,可得
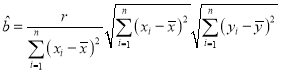
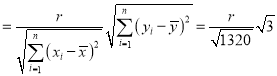
![]() ,
,
![]() ,
,
所求的线性回归方程为![]() .
.
当![]() 时,预报
时,预报![]() .
.
②因为![]() ,所以
,所以![]() ,
,
即该地区身高![]() 的男孩的
的男孩的![]() 的实际值落在区间
的实际值落在区间![]() 内的概率为99.74%,即该地区身高
内的概率为99.74%,即该地区身高![]() 的男孩的
的男孩的![]() 值不在这个区间内的概率极小,仅有0.26%,
值不在这个区间内的概率极小,仅有0.26%,![]() 的
的![]() 值落在该区间内,我们推断他的
值落在该区间内,我们推断他的![]() 值是正常的;
值是正常的;
![]() 的
的![]() 值低于该区间的下限,我们认为他的
值低于该区间的下限,我们认为他的![]() 值是不正常的,建议他去找下引起不正常的原因.
值是不正常的,建议他去找下引起不正常的原因.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】随着经济的快速增长、规模的迅速扩张以及人民生活水平的逐渐提高,日益剧增的垃圾给城市的绿色发展带来了巨大的压力.相关部门在有5万居民的光明社区采用分层抽样方法得到年内家庭人均![]() 与人均垃圾清运量的统计数据如下表:
与人均垃圾清运量的统计数据如下表:
人均 | 3 | 6 | 9 | 12 | 15 |
人均垃圾清运量 | 0.13 | 0.23 | 0.31 | 0.41 | 0.52 |
(1)已知变量![]() 与
与![]() 之间存在线性相关关系,求出其回归直线方程;
之间存在线性相关关系,求出其回归直线方程;
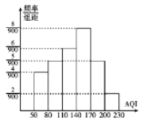
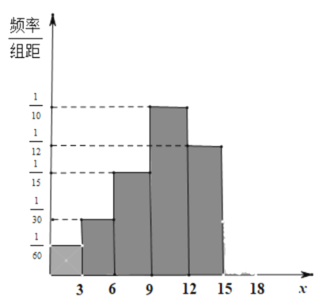
(2)随着垃圾分类的推进,燃烧垃圾发电的热值大幅上升,平均每吨垃圾可折算成上网电量200千瓦时,如图是光明社区年内家庭人均![]() 的频率分布直方图,请补全
的频率分布直方图,请补全![]() 的缺失部分,并利用(1)的结果,估计整个光明社区年内垃圾可折算成的总上网电量.
的缺失部分,并利用(1)的结果,估计整个光明社区年内垃圾可折算成的总上网电量.
参考公式]回归方程![]() ,
,