题目内容
【题目】已知抛物线C:y2=4x的焦点为F,准线为l,过l上一点P作抛物线C的两条切线,切点为A,B.
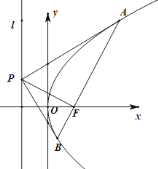
(1)求证:直线AB过焦点F;
(2)若|PA|=8,|PB|=6,求|PF|的值.
【答案】(1)详见解析;(2)![]() .
.
【解析】
(1)设A,B,P的坐标,设直线PA,PB的方程与抛物线联立,求出两根之和及两根之积,由判别式为0及点A,B在抛物线上可得直线PA,PB的斜率与A,B的纵坐标的关系,由于P在两条直线上,可得直线AB的方程ay=﹣2+2x 上,可得直线AB恒过定点(1,0),即直线过抛物线的焦点;
(2)由(1)可得直线AB 的方程,与抛物线联立求出两根之和及两根之积,进而求出直线PA,PB的斜率之积为﹣1,所以直线PA,PB互相垂直,可得弦长|AB|的值,A,B代入抛物线的方程作差可得直线AB的斜率,求出PF的斜率与AB的斜率之积为﹣1,进而求出PF的值.
解:(1)设点A(x1,y1),B(x2,y2),P(﹣1,a)、设直线PA:y﹣y1=k1(x﹣x1),
联立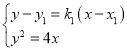 整理可得:y2
整理可得:y2![]() 4x1=0,
4x1=0,
由△=0 得1﹣k1y1+k12x1=0 又y12=4x1,故1﹣k1y1![]() k12y12=0,
k12y12=0,
故(![]() 1)2=0,
1)2=0,
故kPA=k1![]() ,故直线PA的方程为:y﹣y1
,故直线PA的方程为:y﹣y1![]() (x﹣x1),即yy1=2x+2x1,
(x﹣x1),即yy1=2x+2x1,
同理kPB![]() ,直线PB 的方程为:yy2=2x+2x2.
,直线PB 的方程为:yy2=2x+2x2.
又P在直线PA,PB 上∴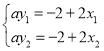 ,
,
故A(x1,y1),B(x2,y2),在直线ay=﹣2+2x 上,
故直线AB 的方程为ay=﹣2+2x.令y=0,得x=1,
∴直线AB过焦点F.
(2)由(1)知联立![]() 消x 得:y2﹣2ay﹣4=0 ,
消x 得:y2﹣2ay﹣4=0 ,
故y1+y2=2a,y1y=﹣4,故kPAkPB![]() 1,
1,
故直线PA与直线![]() 10,
10,
又 ∴y12﹣y22=4(x1﹣x2),kAB
∴y12﹣y22=4(x1﹣x2),kAB![]() ,
,
又kPF![]() ,kPFkAB=﹣1,故PF⊥AB,
,kPFkAB=﹣1,故PF⊥AB,
∴|PF|![]() .
.