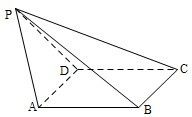
题目内容
已知:点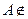 平面
平面 ,求证:过
,求证:过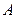 有且只有一个平面
有且只有一个平面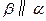 .
.
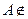 平面
平面 ,求证:过
,求证:过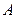 有且只有一个平面
有且只有一个平面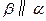 .
.证明见答案
在平面 内任作两条相交直线
内任作两条相交直线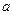 和
和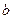 ,则由
,则由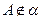 知
知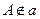 ,
,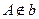 .点
.点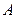 和直线
和直线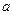 可确定一个平面
可确定一个平面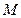 ,点
,点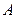 和直线
和直线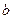 可确定一个平面
可确定一个平面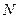 .在平面
.在平面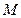 ,
,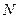 内过
内过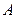 分别作直线
分别作直线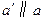 ,
, ,故
,故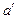 ,
,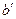 是两条相交直线,可确定一个平面
是两条相交直线,可确定一个平面 .
.
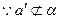 ,
,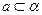 ,
,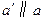 ,
,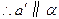 .
.
同理 ,
,
又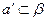 ,
,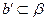 ,
,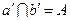 ,
,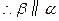 .
.
所以过点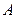 有一个平面
有一个平面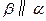 .
.
假设过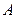 点还有一个平面
点还有一个平面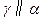 .
.
则在平面 内取一直线
内取一直线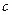 ,
,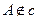 ,点
,点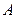 、直线
、直线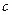 确定一个平面
确定一个平面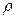 ,由公理
,由公理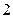 知:
知:
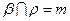 ,
, ,
,
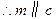 ,
,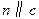 ,
,
又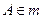 ,
,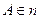 ,
,
这与过一点有且只有一条直线与已知直线平行相矛盾,因此假设不成立,所以平面 只有一个.
只有一个.
所以过平面外一点有且只有一个平面与已知平面平行.
 内任作两条相交直线
内任作两条相交直线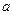 和
和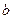 ,则由
,则由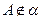 知
知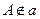 ,
,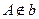 .点
.点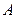 和直线
和直线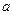 可确定一个平面
可确定一个平面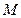 ,点
,点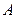 和直线
和直线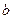 可确定一个平面
可确定一个平面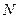 .在平面
.在平面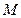 ,
,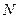 内过
内过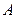 分别作直线
分别作直线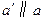 ,
, ,故
,故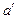 ,
,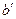 是两条相交直线,可确定一个平面
是两条相交直线,可确定一个平面 .
.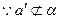 ,
,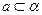 ,
,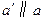 ,
,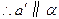 .
.同理
 ,
,又
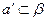 ,
,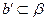 ,
,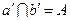 ,
,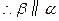 .
.所以过点
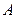 有一个平面
有一个平面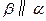 .
.假设过
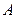 点还有一个平面
点还有一个平面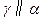 .
.则在平面
 内取一直线
内取一直线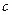 ,
,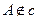 ,点
,点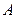 、直线
、直线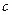 确定一个平面
确定一个平面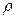 ,由公理
,由公理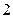 知:
知: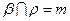 ,
, ,
,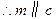 ,
,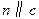 ,
,又
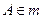 ,
,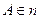 ,
,这与过一点有且只有一条直线与已知直线平行相矛盾,因此假设不成立,所以平面
 只有一个.
只有一个.所以过平面外一点有且只有一个平面与已知平面平行.

练习册系列答案
相关题目
 B
B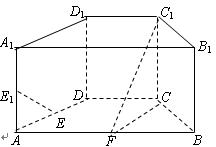
 的顶点
的顶点 与顶点
与顶点 分别在平面
分别在平面 的两侧,且梯形的两边
的两侧,且梯形的两边 与
与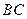 分别与
分别与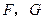 两点;梯形的另两条边
两点;梯形的另两条边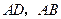 的延长线分别与
的延长线分别与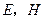 两点,求证:
两点,求证: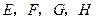 四点共线.
四点共线.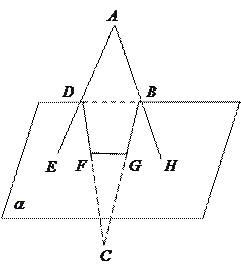
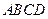 中,
中,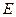 ,
,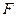 ,
,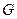 ,
,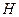 分别是
分别是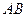 ,
,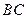 ,
, ,
,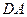 的中点.求证:四边形
的中点.求证:四边形 是平行四边形.
是平行四边形.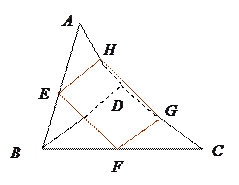
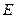 ,
,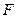 ,
,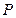 ,
,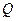 分别是棱长为
分别是棱长为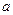 的正方体
的正方体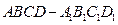 中
中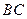 ,
,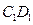 ,
,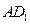 ,
, 的中点.
的中点. 平面
平面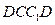 ;
;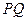 长;
长;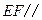 平面
平面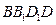 .
.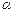 外有两条直线
外有两条直线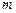 和
和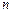 ,如果
,如果 和
和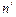 ,给出下列四个命题:
,给出下列四个命题: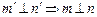

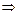
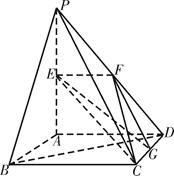 如图,平面
如图,平面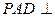 平面ABCD,
平面ABCD,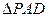 是直角三角形,
是直角三角形, ,E、F、G分别是
,E、F、G分别是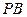 ∥面EFC;
∥面EFC;