题目内容
已知函数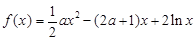 ,其中常数
,其中常数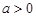 .
.
(1)求 的单调区间;
的单调区间;
(2)如果函数 在公共定义域D上,满足
在公共定义域D上,满足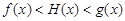 ,那么就称
,那么就称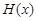 为
为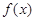 与
与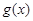 的“和谐函数”.设
的“和谐函数”.设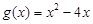 ,求证:当
,求证:当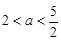 时,在区间
时,在区间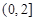 上,函数
上,函数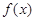 与
与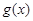 的“和谐函数”有无穷多个.
的“和谐函数”有无穷多个.
(1) ,
,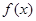 的单调递增区间是
的单调递增区间是 和
和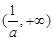 ,单调递减区间是
,单调递减区间是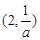
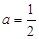 ,单调递增区间是
,单调递增区间是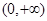 ,
,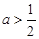 ,单调递增区间是
,单调递增区间是 和
和 ,单调递减区间是
,单调递减区间是
(2)作差构造新函数证明.
解析试题分析:(1)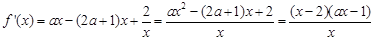
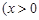 ,常数
,常数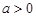 )
)
令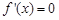 ,则
,则 ,
,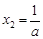
①当 时,
时,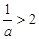 ,
,
在区间 和
和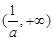 上,
上, ;在区间
;在区间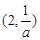 上
上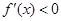 ,
,
故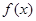 的单调递增区间是
的单调递增区间是 和
和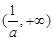 ,单调递减区间是
,单调递减区间是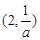
②当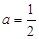 时,
时,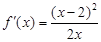 ,故
,故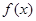 的单调递增区间是
的单调递增区间是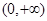
③当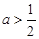 时,
时,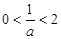 ,
,
在区间 和
和 上,
上, ;在区间
;在区间 上
上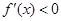 ,
,
故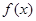 的单调递增区间是
的单调递增区间是 和
和 ,单调递减区间是
,单调递减区间是
(2)令 ,
,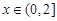

令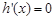 ,则
,则 ,
,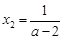
因为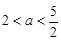 ,所以
,所以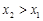 ,且
,且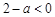
从而在区间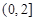 上,
上,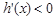 ,即
,即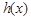 在
在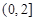 上单调递减
上单调递减
所以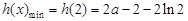
又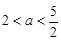 ,所以
,所以 ,即
,即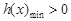
设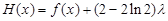 (
( ,则
,则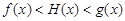
所以在区间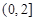 上,函数
上,函数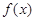 与
与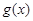 的“和谐函数”有无穷多个
的“和谐函数”有无穷多个
考点:类比推理;函数的定义域及其求法;函数的值域;函数单调性的判断与证明;函数单调性的性质.
点评:本题主要以新定义为载体,综合考查了函数的单调性、函数的最值方程的根的情况、二次函数的最值的求解,考查了利用已学知识解决新问题的能力,考查了推理运算的能力,本题综合性较强.

练习册系列答案
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案
相关题目
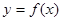 的图像在
的图像在 处的切线方程;
处的切线方程; ,求函数
,求函数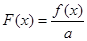 在
在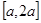 上的最小值.
上的最小值.
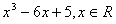 .
. 的单调区间和极值。
的单调区间和极值。 的方程
的方程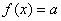 有三个不同实根,求实数
有三个不同实根,求实数 的取值范围;
的取值范围;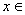 (1,+∞)时,
(1,+∞)时,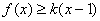 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.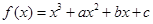 在
在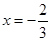 与
与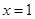 时都取得极值.
时都取得极值. 的值与函数
的值与函数 的单调区间;
的单调区间;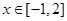 ,不等式
,不等式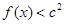 恒成立,求
恒成立,求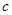 的取值范围.
的取值范围.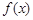 的导函数是
的导函数是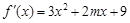 ,
,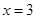 处取得极值,且
处取得极值,且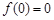 ,
, 上的最大值为
上的最大值为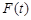 ,若对任意的
,若对任意的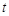
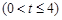 总有
总有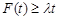 成立,求
成立,求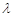 的取值范围;
的取值范围;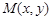 是曲线
是曲线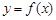 上的任意一点.当
上的任意一点.当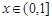 时,求直线OM斜率的最
时,求直线OM斜率的最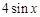 的大小关系,并说明理由.
的大小关系,并说明理由.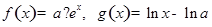 ,其中
,其中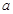 为常数,且函数
为常数,且函数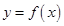 和
和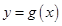 的图象在其与坐标轴的交点处的切线互相平行,求此时平行线的距离。
的图象在其与坐标轴的交点处的切线互相平行,求此时平行线的距离。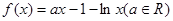
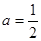 时,求函数在
时,求函数在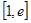 上的最大值和最小值;
上的最大值和最小值;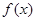 在
在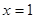 处取得极值,不等式
处取得极值,不等式 对
对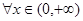 恒成立,求实数
恒成立,求实数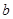 的取值范围。
的取值范围。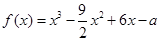 .
.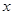 ,
,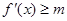 恒成立,求
恒成立,求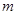 的最大值;
的最大值;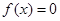 有且仅有一个实根,求
有且仅有一个实根,求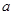 的取值范围.
的取值范围.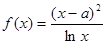 (其中
(其中 为常数).
为常数). 时,求函数的单调区间;
时,求函数的单调区间; 时,设函数
时,设函数 的3个极值点为
的3个极值点为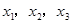 ,且
,且 .
. .
.