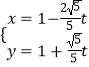题目内容
【题目】设函数 ![]() (
( ![]() 为常数,e=2.71828……是自然对数的底数).
为常数,e=2.71828……是自然对数的底数).
(1)当 ![]() 时,求函数
时,求函数 ![]() 的单调区间;
的单调区间;
(2)若函数 ![]() 在
在 ![]() 内存在两个极值点,求
内存在两个极值点,求 ![]() 的取值范围.
的取值范围.
【答案】
(1)解:函数 ![]() 的定义域为
的定义域为 ![]()
![]()
由 ![]() 可得
可得 ![]() ,
,
所以当 ![]() 时,
时, ![]() ,函数
,函数 ![]() 单调递减;
单调递减;
当 ![]() 时,
时, ![]() ,函数
,函数 ![]() 单调递增;
单调递增;
所以 ![]() 的单调递减区间为
的单调递减区间为 ![]() 单调递增区间为
单调递增区间为 ![]()
(2)解:由1知, ![]() 时,函数
时,函数 ![]() 在
在 ![]() 内单调递减,
内单调递减,
故 ![]() 在
在 ![]() 内不存在极值点;
内不存在极值点;
当 ![]() 时,设函数
时,设函数 ![]() ,,
,,
因为 ![]() ,
,
当 ![]() 时,当
时,当 ![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
故 ![]() 在
在 ![]() 内不存在两个极值点;
内不存在两个极值点;
当 ![]() 时,得
时,得 ![]() 时,
时, ![]() ,函数
,函数 ![]() 单调递减;
单调递减;
![]() 时,
时, ![]() ,函数
,函数 ![]() 单调递增;
单调递增;
所以函数 ![]() 的最小值为
的最小值为 ![]() ,
,
函数 ![]() 在
在 ![]() 内存在两个极值点,
内存在两个极值点,
当且仅当 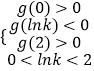 ,解得
,解得 ![]() .
.
综上所述,函数 ![]() 在
在 ![]() 内存在两个极值点时,k的取值范围为
内存在两个极值点时,k的取值范围为 ![]()
【解析】(1)根据题意结合已知条件求出原函数的导函数利用导函数在指定区间上的的正负情况得出原函数的增减性以及增减区间。(2)函数f(x) 在( 0 , 2 ) 内存在两个极值点,等价于它的导函数f‘(x) 在 ( 0 , 2 ) 内存在两个不同的零点。
【考点精析】掌握利用导数研究函数的单调性和函数的零点是解答本题的根本,需要知道一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.
在这个区间单调递减;函数的零点就是方程的实数根,亦即函数的图象与轴交点的横坐标.即:方程有实数根,函数的图象与坐标轴有交点,函数有零点.

 阅读快车系列答案
阅读快车系列答案【题目】某电脑公司有6名产品推销员,其中工作年限与年推销金额数据如下表:
推销员编号 | 1 | 2 | 3 | 4 | 5 |
工作年限 | 3 | 5 | 6 | 7 | 9 |
推销金额 | 2 | 3 | 4 | 5 | 6 |
(1)请画出上表数据的散点图;

(2)求年推销金额![]() 关于工作年限
关于工作年限![]() 的线性回归方程;
的线性回归方程;
(3)若第6名推销员的工作年限为11年,试估计他的年推销金额.
 ,
,![]() .
.