题目内容
【题目】已知数列{an}的首项a1=a,其前n项和为Sn , 且满足Sn+Sn﹣1=3n2+2n+4(n≥2),若对任意的n∈N* , an<an+1恒成立,则a的取值范围是( )
A.( ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.(﹣∞, ![]() )
)
【答案】C
【解析】解:由Sn+Sn﹣1=3n2+2n+4(n≥2),可以得到Sn+1+Sn=3(n+1)2+2(n+1)+4, 两式相减得an+1+an=6n+5,
故an+2+an+1=6n+11,两式再相减得an+2﹣an=6,
由n=2得a1+a2+a1=20,a2=20﹣2a,
故偶数项为以20﹣2a为首项,以6为公差的等差数列,
从而a2n=6n+14﹣2a;
n=3得a1+a2+a3+a1+a2=37,a3=2a﹣3,
从而a2n+1=6n﹣9+2a,
由条件得 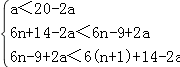 ,
,
解得 ![]() <a<
<a< ![]() ,
,
故选:C.
【考点精析】本题主要考查了数列的通项公式的相关知识点,需要掌握如果数列an的第n项与n之间的关系可以用一个公式表示,那么这个公式就叫这个数列的通项公式才能正确解答此题.

 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案【题目】某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生. 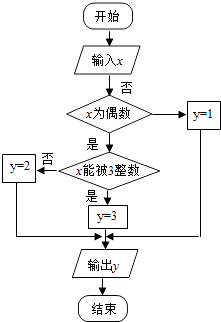
(1)分别求出按程序框图正确编程运行时输出y的值为i的概率Pi(i=1,2,3);
(2)甲、乙两同学依据自己对程序框图的理解,各自编写程序重复运行n次后,统计记录了输出y的值为i(i=1,2,3)的频数.以下是甲、乙所作频数统计表的部分数据.
甲的频数统计表(部分)
运行 | 输出y的值 | 输出y的值 | 输出y的值 |
30 | 14 | 6 | 10 |
… | … | … | … |
2100 | 1027 | 376 | 697 |
乙的频数统计表(部分)
运行 | 输出y的值 | 输出y的值 | 输出y的值 |
30 | 12 | 11 | 7 |
… | … | … | … |
2100 | 1051 | 696 | 353 |
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编写程序符合算法要求的可能性较大.
