Question

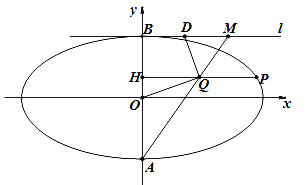
【题目】如图所示，椭圆的短轴为，，离心率，为第一象限内椭圆上的任意一点，设轴于，为线段的中点，过作直线轴．

（1）求椭圆的方程；

（2）若的纵坐标为，求直线截椭圆所得的弦长；

（3）若直线交直线于，为直线上一点，且为原点），证明：为线段的中点．

Answer 1

【答案】(1) ；(2) ；(3)见解析.

【解析】

（1）先求出b＝1，再根据离心率公式和a2＝b2+c2，即可求出，

（2）根据弦长公式即可求出，

（3）设P（x0，y0），求出点M和D的坐标根据DQ⊥OQ（O为原点）即可证明．

(1)

,则,a=2

椭圆C的方程为：

(2)由点P在椭圆上，则,可得

，，

直线AQ:y=x-1

代入，整理可得：

从而所截弦长为

(3)设P()，则Q, ①

直线AQ:y=x-1,与直线l:y=1联立

可得=

设D(),由DQ，可得

解得，代入①式中，化简

则

代入①式中，则，得证.