题目内容
已知圆 的方程:
的方程:
(1)求m的取值范围;
(2)若圆C与直线 相交于
相交于 ,
, 两点,且
两点,且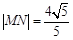 ,求
,求 的值
的值
(3)若(1)中的圆与直线x+2y-4=0相交于M、N两点,且OM⊥ON(O为坐标原点),求m的值;
(1)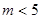 ;(2)
;(2) ;(3)
;(3) .
.
解析试题分析:(1)圆的方程要满足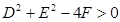 ;或配成圆的标准方程,
;或配成圆的标准方程, ;
;
(2) 利用弦心距公式,先求点到面的距离,利用 ,求出
,求出 的值;
的值;
(3)设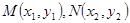 ,若
,若 ,那么
,那么 ,利用直线方程与圆的方程联立,得到根与系数的关系式,代入后,求得
,利用直线方程与圆的方程联立,得到根与系数的关系式,代入后,求得 的值.
的值.
试题解析:解:(1)(1)方程x2+y2-2x-4y+m=0,可化为
(x-1)2+(y-2)2=5-m,
∵此方程表示圆,
∴5-m>0,即m<5.
(2) 圆的方程化为  ,圆心 C(1,2),半径
,圆心 C(1,2),半径  ,
,
则圆心C(1,2)到直线 的距离为
的距离为 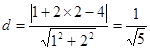
由于 ,则
,则 ,有
,有 ,
, 得
得 .
.
(3)
消去x得(4-2y)2+y2-2×(4-2y)-4y+m=0,
化简得5y2-16y+m+8=0.
设M(x1,y1),N(x2,y2),则
 ①②
①②
由OM⊥ON得y1y2+x1x2=0
即y1y2+(4-2y1)(4-2y2)=0,
∴16-8(y1+y2)+5y1y2=0.
将①②两式代入上式得
16-8× +5×
+5×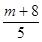 =0,
=0,
解之得 .
.
考点:1.圆的方程;2.直线与圆的位置关系.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 ,圆
,圆 .
. 被圆
被圆 所截得的弦长;
所截得的弦长; 的直线
的直线 与直线
与直线 垂直,
垂直, 上的圆
上的圆 相切,圆
相切,圆 ,求圆
,求圆 ,求圆C方程.
,求圆C方程.
 为圆心的圆与直线
为圆心的圆与直线 相切,过点
相切,过点 的动直线与圆
的动直线与圆 相交于
相交于 两点.
两点. 时,求直线
时,求直线 的方程.
的方程. +y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点.
+y2=1的左、右焦点,F1,F2关于直线x+y-2=0的对称点是圆C的一条直径的两个端点.