题目内容
【题目】在某市高三教学质量检测中,全市共有5000名学生参加了本次考试,其中示范性高中参加考试学生人数为2000人,非示范性高中参加考试学生人数为3000人.现从所有参加考试的学生中随机抽取100人,作检测成绩数据分析.

(1)设计合理的抽样方案(说明抽样方法和样本构成即可);
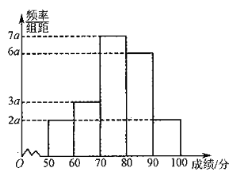
(2)依据100人的数学成绩绘制了如图所示的频率分布直方图,据此估计本次检测全市学生数学成绩的平均分;
(3)如果规定成绩不低于130分为特别优秀,现已知语文特别优秀占样本人数的![]() ,语文、数学两科都特别优秀的共有3人,依据以上样本数据,完成列联表,并分析是否有
,语文、数学两科都特别优秀的共有3人,依据以上样本数据,完成列联表,并分析是否有![]() 的把握认为语文特别优秀的同学,数学也特别优秀.
的把握认为语文特别优秀的同学,数学也特别优秀.
语文特别优秀 | 语文不特别优秀 | 合计 | |
数学特别优秀 | |||
数学不特别优秀 | |||
合计 |
参考公式:![]()
参考数据:
| 0.50 | 0.40 | … | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | … | 6.635 | 7.879 | 10.828 |
【答案】(1)采用分层抽样,示范性高中抽取![]() 人,非示范性高中抽
人,非示范性高中抽![]() 人;(2)
人;(2)![]() ;(3)有
;(3)有![]() 的把握认为语文特别优秀的同学,数学也特别优秀.
的把握认为语文特别优秀的同学,数学也特别优秀.
【解析】
(1)由于总体有明显差异的两部分构成,故采用分层抽样,根据分层抽样的计算方法,即可求解;
(2)由频率分布直方图,利用平均数的计算公式,即可求解.
(3)由题意,得出![]() 的列联表,利用卡方的计算公式,求得卡方值,即可得出结论.
的列联表,利用卡方的计算公式,求得卡方值,即可得出结论.
(1)由于总体有明显差异的两部分构成,故采用分层抽样,
由题意,从示范性高中抽取![]() 人,从示师范性高中抽取
人,从示师范性高中抽取![]() 人
人
(2)由频率分布直方图估算样本平均分为
![]() ,
,
推测估计本次检测全市学生数学平均分为![]()
(3)由题意,语文特别优秀学生有![]() 人 ,数学特别优秀的学生有
人 ,数学特别优秀的学生有![]() 人
人
因为语文、数学都特别优秀的共有![]() 人,故列联表如下:
人,故列联表如下:
语文特别优秀 | 语文不特别优秀 | 合计 | |
数学特别优秀 | 3 | 1 | 4 |
数学不特别优秀 | 2 | 94 | 96 |
合计 | 5 | 95 | 100 |
![]() ,
,
所以有![]() 的把握认为语文特别优秀的同学,数学也特别优秀.
的把握认为语文特别优秀的同学,数学也特别优秀.

 阅读快车系列答案
阅读快车系列答案