题目内容
【题目】已知动圆过定点A(4,0), 且在y轴上截得的弦MN的长为8.
(Ⅰ) 求动圆圆心的轨迹C的方程;
(Ⅱ) 已知点B(-1,0), 设不垂直于x轴的直线l与轨迹C交于不同的两点P, Q, 若x轴是![]() 的角平分线, 证明直线l过定点.
的角平分线, 证明直线l过定点.
【答案】(Ⅰ)![]() (
(![]() ) (Ⅱ)见解析
) (Ⅱ)见解析
【解析】(Ⅰ)设动圆圆心C的坐标为( x , y )则![]() 所以,所求动圆圆心的轨迹C的方程为
所以,所求动圆圆心的轨迹C的方程为![]() (
(![]() )
)
(Ⅱ)证明:
设直线l方程为![]() ,联立
,联立![]() 得
得![]() (其中
(其中![]() )
)
设![]() ,若x轴是
,若x轴是![]() 的角平分线,则
的角平分线,则
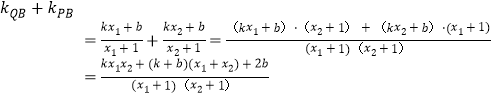
![]() ,即
,即![]() 故直线l方程为
故直线l方程为![]() ,直线l过定点.(1,0)
,直线l过定点.(1,0)
本题考查轨迹方程求法、直线方程、圆方程、直线与圆的位置关系及直线过定点问题.第一问曲线轨迹方程的求解问题是高考的热点题型之一,准确去除不满足条件的![]() 点是关键.第二问对角平分线的性质运用是关键,对求定值问题的解决要控制好运算量,同时注意好判别式
点是关键.第二问对角平分线的性质运用是关键,对求定值问题的解决要控制好运算量,同时注意好判别式![]() 的条件,以防多出结果.圆锥曲线问题经常与向量、三角函数结合,在训练中要注意.本题无论是求圆心的轨迹方程,还是求证直线过定点,计算量都不太大,对思维的要求挺高;设计问题背景,彰显应用魅力.
的条件,以防多出结果.圆锥曲线问题经常与向量、三角函数结合,在训练中要注意.本题无论是求圆心的轨迹方程,还是求证直线过定点,计算量都不太大,对思维的要求挺高;设计问题背景,彰显应用魅力.

练习册系列答案
相关题目