Question

19．已知α∥β∥γ，直线a与b分别交α，β，γ于点A，B，C和D，E，F，且AB=2，BC=3，DE=4，则EF=6．

Answer 1

分析 若A，B，C，D，E，F，六点共面，由面面平行的性质定理和平行线分线段成比例定理可得$\frac{2}{3}=\frac{4}{EF}$，由此能求出EF；若A，B，C，D，E，F，六点不共面，连接AF，交β于M，平面ACF分别交β、γ于BM、CF，也能推导出$\frac{2}{3}=\frac{4}{EF}$，从而求出EF．

解答 解：∵AB=2，BC=3，DE=4，
若A，B，C，D，E，F，六点共面
由面面平行的性质定理可得
AB∥CD∥EF
根据平行线分线段成比例定理可得：
$\frac{AB}{BC}=\frac{DE}{EF}$，即$\frac{2}{3}=\frac{4}{EF}$，解得EF=6
若A，B，C，D，E，F，六点不共面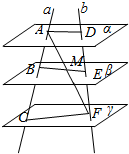
连接AF，交β于M
连接BM、EM、BE．
∵β∥γ，平面ACF分别交β、γ于BM、CF，
∴BM∥CF．
∴$\frac{AB}{BC}=\frac{AM}{MF}$，同理，$\frac{AM}{MF}=\frac{DE}{EF}$．
∴$\frac{AB}{BC}=\frac{DE}{EF}$，即$\frac{2}{3}=\frac{4}{EF}$，解得EF=6
综上所述：EF=6．
故答案为：6．

点评 本题考查线段长的求法，是中档题，解题时要认真审题，注意面面平行的性质定理和平行线分线段成比例定理的合理运用．