题目内容
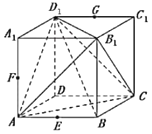
【题目】四棱柱![]() 中,底面
中,底面![]() 为正方形,
为正方形, ![]() 平面
平面![]() 为棱
为棱![]() 的中点,
的中点, ![]() 为棱
为棱![]() 的中点,
的中点, ![]() 为棱
为棱![]() 的中点.
的中点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,棱
,棱![]() 上有一点
上有一点![]() ,且
,且![]() ,使得二面角
,使得二面角![]() 的余弦值为
的余弦值为![]() ,求
,求![]() 的值.
的值.

【答案】(1)见解析;(2) ![]() .
.
【解析】试题分析: ![]() 四边形
四边形![]() 为平行四边形得
为平行四边形得![]() ,由中点得
,由中点得![]() ,
,
又![]() ,
, ![]() 得证
得证 ![]() 以
以![]() 为原点,
为原点, ![]() 方向分别为
方向分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴正方向,建立如图所示的空间垂直坐标系,求平面
轴正方向,建立如图所示的空间垂直坐标系,求平面![]() 的一个法向量为
的一个法向量为![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,代入公式求出结果
,代入公式求出结果
解析:(1)![]() 分别为棱
分别为棱![]() 中点,
中点,
![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,
为平行四边形,
![]() ,
,
又![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
![]() 为棱
为棱![]() 的中点,
的中点,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
又![]() ,
,
![]() 平面
平面![]() .
.
(2)由题意知![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点, ![]() 方向分别为
方向分别为![]() 轴、
轴、![]() 轴、
轴、![]() 轴正方向,建立如图所示的空间垂直坐标系,
轴正方向,建立如图所示的空间垂直坐标系,
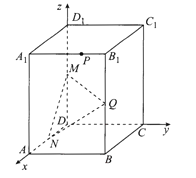
设![]() ,则
,则![]() ,
,
设![]() ,则由
,则由![]() ,
,
得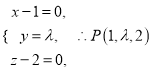 ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则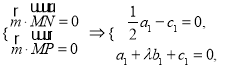 取
取![]() ,
,
则![]() ,
,
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则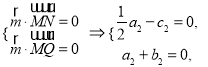 取
取![]() ,
,
则![]() ,
,
由题知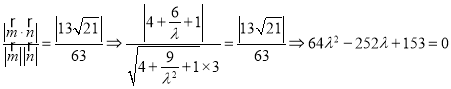 ,
,
解得![]() 或
或![]() (与
(与![]() 矛盾,舍去),
矛盾,舍去),
故![]() .
.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
【题目】探究函数![]() 的图象与性质.
的图象与性质.
(1)下表是y与x的几组对应值.
| … |
|
|
|
|
|
|
| … |
| … |
|
|
|
|
|
|
| … |
其中m的值为_______________;
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并已画出了函数图象的一部分,请你画出该图象的另一部分;
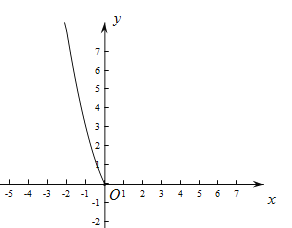
(3)结合函数的图象,写出该函数的一条性质:_________;
(4)若关于x的方程![]() 有2个实数根,则t的取值范围是______.
有2个实数根,则t的取值范围是______.