题目内容
在一般情况下,大桥上的车流速度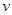 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到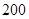 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 ;当
;当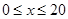 时,车流速度为
时,车流速度为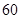 千米/小时.研究表明:当
千米/小时.研究表明:当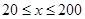 时,车流速度
时,车流速度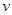 是车流密度
是车流密度 的一次函数.
的一次函数.
(1)当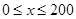 时,求函数
时,求函数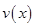 的表达式;
的表达式;
(2)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)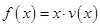 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时)
(1)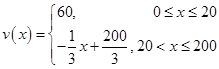 ;
;
(2)当车流密度为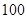 辆/千米时,车流量达到最大,且最大值约
辆/千米时,车流量达到最大,且最大值约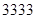 辆/小时.
辆/小时.
解析试题分析:(1)先根据题中函数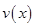 在区间
在区间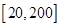 上为一次函数,设
上为一次函数,设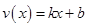 ,利用
,利用 和
和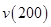 的值列方程组解出
的值列方程组解出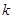 和
和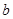 的值,从而确定函数
的值,从而确定函数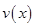 的解析式;(2)利用(1)中函数
的解析式;(2)利用(1)中函数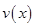 的解析式,将函数
的解析式,将函数 的解析式确定下来(分段函数),然后分别求出函数
的解析式确定下来(分段函数),然后分别求出函数 在区间
在区间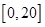 与
与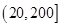 上的最大值,并比较大小,从而确定函数
上的最大值,并比较大小,从而确定函数 在定义域
在定义域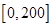 的最大值,进而确定相应的车流密度与车流量.
的最大值,进而确定相应的车流密度与车流量.
试题解析:(1)当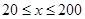 时,设
时,设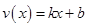 ,
,
则有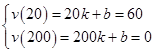 ,解得
,解得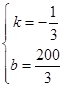 ,
,
所以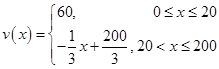 ;
;
(2)由题意知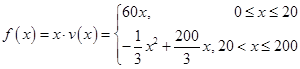 ,
,
当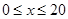 时,
时,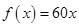 ,则函数
,则函数 在区间
在区间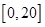 上单调递增,此时
上单调递增,此时 在
在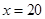 处取最大值,
处取最大值,
即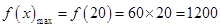 ;
;
当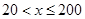 时,
时,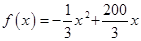 ,函数图象开口朝上,对称轴为直线
,函数图象开口朝上,对称轴为直线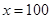 ,
,
此时函数 在
在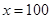 处取得最大值,即
处取得最大值,即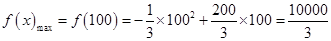 ,
,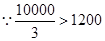 ,故当
,故当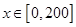 时,
时,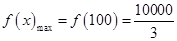 ,
,
即当车流密度为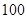 辆/千米时,车流量达到最大,且最大值约
辆/千米时,车流量达到最大,且最大值约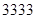 辆/小时.
辆/小时.
考点:1.函数解析式;2.分段函数的最值

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
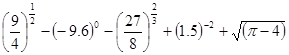 ;
;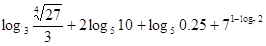 .
.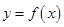 和
和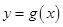 的图象关于
的图象关于 轴对称,且
轴对称,且 .
.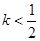 时,解不等式
时,解不等式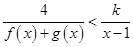 .
.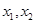 是关于
是关于 的方程
的方程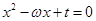 的两个根,且
的两个根,且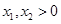 .
.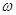 与
与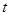 之间满足的关系式;
之间满足的关系式;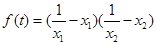 ,若存在
,若存在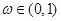 ,使不等式
,使不等式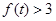 在其定义域范围内恒成立,求
在其定义域范围内恒成立,求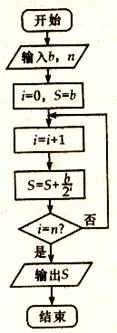
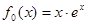 ,
,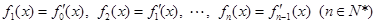 .
.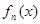 的表达式(不需证明);
的表达式(不需证明);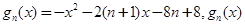 的最大值为
的最大值为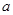 ,
,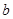 ,求
,求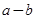 的最小值.
的最小值.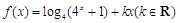 是偶函数.
是偶函数.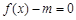 有解,求m的取值范围.
有解,求m的取值范围.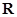 上的单调函数
上的单调函数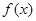 满足
满足 ,且对任意
,且对任意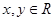 都有
都有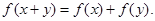
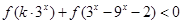 对任意
对任意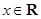 恒成立,求实数
恒成立,求实数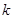 的取值范围.
的取值范围. 小时的收费为
小时的收费为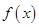 元
元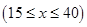 ,在乙家租一张球台开展活动
,在乙家租一张球台开展活动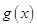 元
元