题目内容
设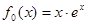 ,
,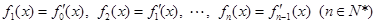 .
.
(1)请写出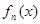 的表达式(不需证明);
的表达式(不需证明);
(2)求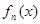 的极小值;
的极小值;
(3)设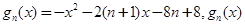 的最大值为
的最大值为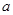 ,
,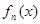 的最小值为
的最小值为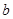 ,求
,求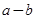 的最小值.
的最小值.
(1)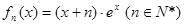 ;(2)
;(2)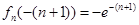 ;(3)
;(3)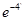 .
.
解析试题分析: (1)依次求出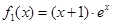 ,
,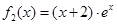 ,
,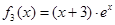 ,
,
由此便可猜测出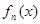 的表达式
的表达式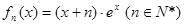 .
.
(2)要求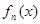 的极小值,先求出
的极小值,先求出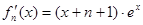 ,
,
由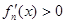 ,
,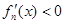 可得
可得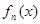 的单调区间和极值.
的单调区间和极值.
(3)配方法可以求出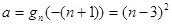 .
.
由(2)得: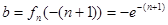 ,所以
,所以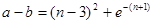 .
.
问题转化为求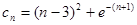 的最小值.这又有两种方法:
的最小值.这又有两种方法:
法一、构造函数,通过求导来求它的最小值;法二、通过研究这个数列的单调性来求它的最小值.
试题解析:(1)根据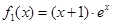 ,
,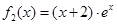 ,
,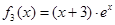 ,
,
猜测出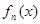 的表达式
的表达式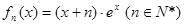 . 4分
. 4分
(2)求导得: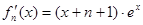 ,
,
因为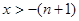 时,
时,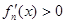 ;当
;当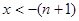 时,
时,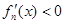 .
.
所以,当 时,
时,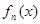 取得极小值
取得极小值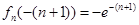 ,
,
即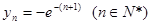 . 8分
. 8分
(3)将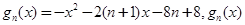 配方得
配方得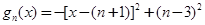 ,
,
所以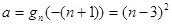 .
.
又因为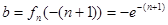 ,所以
,所以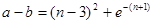 ,10分
,10分
问题转化为求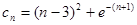 的最小值.
的最小值.
解法1(构造函数):
令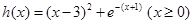 ,
,
则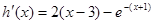 ,又
,又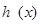 在区间
在区间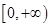 上单调递增,
上单调递增,
所以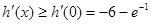 .
.
又因为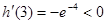 ,
,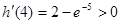 ,
,
所以存在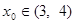 使得
使得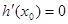 .
.
又有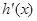 在区间
在区间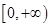 上单调递增,所以
上单调递增,所以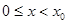 时,
时,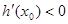 ;
;
当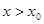 时,
时,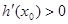 ,
,
即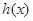 在区间
在区间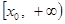 上单调递增,在区间
上单调递增,在区间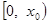 上单调递减,
上单调递减,
所以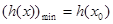 .
.
又由于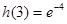 ,
, ,
,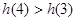 ,
,
所以当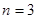 时,
时,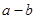 取得最小值
取得最小值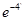 .
.
解法2(利用数列的单调性):
因为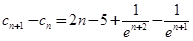 ,
,
当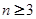 时,
时,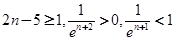 ,
,
所以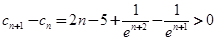 ,所以
,所以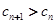 .
.
又因为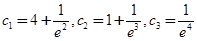 ,
,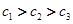 .
.
所以当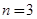 时,
时,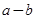 取得最小值
取得最小值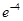 .14分
.14分
考点:1、归纳推理;2、导数的应用;3、函数的最值.

练习册系列答案
相关题目
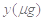 与服药后的时间
与服药后的时间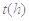 之间近似满足如图所示的曲线.其中
之间近似满足如图所示的曲线.其中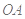 是线段,曲线段
是线段,曲线段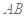 是函数
是函数
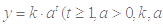 是常数
是常数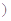 的图象.
的图象.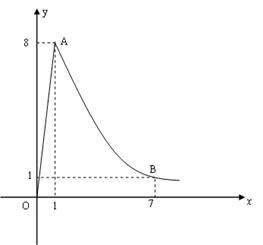
 关于时间
关于时间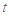 的函数关系式;
的函数关系式;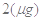 时治疗有效,假若某病人第一次服药为早上
时治疗有效,假若某病人第一次服药为早上 ,为保持疗效,第二次服药最迟是当天几点钟?
,为保持疗效,第二次服药最迟是当天几点钟?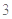
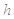 ,该病人每毫升血液中含药量为多少
,该病人每毫升血液中含药量为多少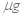 ?
?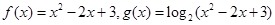 ,且两函数定义域均为
,且两函数定义域均为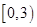 ,
, 在定义域内的图像,并求
在定义域内的图像,并求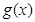 的值域.(5分)
的值域.(5分)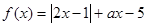 (a是常数,a∈R)
(a是常数,a∈R)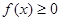 的解集;
的解集;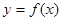 恰有两个不同的零点,求a的取值范围.
恰有两个不同的零点,求a的取值范围.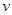 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到
(单位:辆/千米)的函数.当桥上的车流密度达到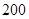 辆/千米时,造成堵塞,此时车流速度为
辆/千米时,造成堵塞,此时车流速度为 ;当
;当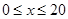 时,车流速度为
时,车流速度为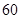 千米/小时.研究表明:当
千米/小时.研究表明:当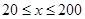 时,车流速度
时,车流速度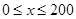 时,求函数
时,求函数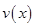 的表达式;
的表达式;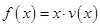 可以达到最大,并求出最大值.(精确到1辆/小时)
可以达到最大,并求出最大值.(精确到1辆/小时) 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为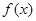 万元,且
万元,且
 (万元)关于年产品
(万元)关于年产品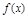 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m. (单位:千克)与销售价格
(单位:千克)与销售价格 (单位:元/千克)满足关系式
(单位:元/千克)满足关系式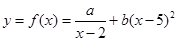 ,其中
,其中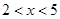 ,
, 为常数,已知销售价格为4元/千克时,每日可销售出该商品5千克;销售价格为4.5元/千克时,每日可销售出该商品2.35千克.
为常数,已知销售价格为4元/千克时,每日可销售出该商品5千克;销售价格为4.5元/千克时,每日可销售出该商品2.35千克. 的解析式;
的解析式; x2-x+
x2-x+ 是[1,b]上的“四维光军”函数,求常数b的值;
是[1,b]上的“四维光军”函数,求常数b的值;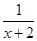 是区间[a,b]上的“四维光军”函数?若存在,求出a,b的值,否则,请说明理由.
是区间[a,b]上的“四维光军”函数?若存在,求出a,b的值,否则,请说明理由.