题目内容
【题目】已知函数![]() 将
将![]() 的图象向右平移两个单位,得到函数
的图象向右平移两个单位,得到函数![]() 的图象.
的图象.
(1)求函数![]() 的解析式;
的解析式;
(2)若方程![]() 在
在![]() 上有且仅有一个实根,求
上有且仅有一个实根,求![]() 的取值范围;
的取值范围;
(3)若函数![]() 与
与![]() 的图象关于直线
的图象关于直线![]() 对称,设
对称,设![]() ,已知
,已知![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(Ⅰ)由图象的平移可得g(x)的解析式;
(Ⅱ)设![]() ,问题转化为
,问题转化为![]() 在t∈[1,2]上有且仅有一个实根,通过分类讨论的思想得到结果;
在t∈[1,2]上有且仅有一个实根,通过分类讨论的思想得到结果;
(Ⅲ)设![]() ,t∈(2,+∞).问题转化为t2﹣4at+4a>0对任意t∈(2,+∞)恒成立,变量分离后构造函数
,t∈(2,+∞).问题转化为t2﹣4at+4a>0对任意t∈(2,+∞)恒成立,变量分离后构造函数![]() ,可得其最小值,进而可得答案.
,可得其最小值,进而可得答案.
试题解析:
(1) ![]()
(2)设![]() ,则
,则![]() ,原方程可化为
,原方程可化为![]()
于是只须![]() 在
在![]() 上有且仅有一个实根,
上有且仅有一个实根,
法1:设![]() ,对称轴t=
,对称轴t=![]() ,则
,则![]() ① , 或
① , 或 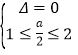 ②
②
由①得 ![]() ,即
,即![]() ,
, ![]()
由②得![]() 无解, ,则
无解, ,则![]() 。
。
法2:由![]() ,得,
,得, ![]() ,
, ![]() ,
,
设![]() ,则
,则![]() ,
, ![]() ,记
,记![]() ,
,
则![]() 在
在![]() 上是单调函数,因为故要使题设成立,
上是单调函数,因为故要使题设成立,
只须![]() ,即
,即![]() ,
,
从而有![]()
(3)设![]() 的图像上一点
的图像上一点![]() ,点
,点![]() 关于
关于![]() 的对称点为
的对称点为![]() ,
,
由点![]() 在
在![]() 的图像上,所以
的图像上,所以![]() ,
,
于是![]() 即
即![]() .
. ![]() .
.
由![]() ,化简得
,化简得![]() ,设
,设![]() ,即
,即![]() 恒成立.
恒成立.
注意到t﹣1>1,分离参数得![]() 对任意t∈(2,+∞)恒成立.
对任意t∈(2,+∞)恒成立.
设![]() , t∈(2,+∞),即
, t∈(2,+∞),即![]()
而![]() .
.
可证m(t)在(2,+∞)上单调递增.
∴m(t)>m(2)=4,
∴![]() ,即a∈(﹣∞,1].
,即a∈(﹣∞,1].

练习册系列答案
相关题目
