题目内容

【题目】在某大学联盟的自主招生考试中，报考文史专业的考生参加了人文基础学科考试科目“语文”和“数学”的考试.某考场考生的两科考试成绩数据统计如下图所示，本次考试中成绩在内的记为，其中“语文”科目成绩在内的考生有10人.

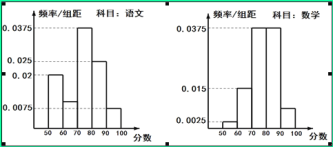
（1）求该考场考生数学科目成绩为的人数；

（2）已知参加本考场测试的考生中，恰有2人的两科成绩均为.在至少一科成绩为的考生中，随机抽取2人进行访谈，求这2人的两科成绩均为的概率.

【答案】(1)3;(2).

【解析】

试题分析：(1)频率分布直方图中面积表示频率，设频率=,为总人数，所以，结合的频率，；

(2)首先算出语文与数学中成绩为的人数，通过列举的方法计算出选出的2人所有可能的情况及这两人的两科成绩等级均为的情况；利用古典概型概率公式求出随机抽取两人进行访谈，这两人的两科成绩等级均为的概率。

试题解析：（1）该考场的考生人数为10÷0.25=40人. 2分

数学科目成绩为的人数为

40×(1-0.0025×10-0.015×10-0.0375×10×2)=40×0.075=3人. 6分

（2）语文和数学成绩为A的各有3人，其中有两人的两科成绩均为，所以还有两名同学只有一科成绩为. 8分

设这四人为甲、乙、丙、丁，其中甲、乙的两科成绩均为，则在至少一科成绩为的考生中，随机抽取两人进行访谈，基本事件为{甲，乙}，{甲，丙}，{甲，丁}，{乙，丙}，{乙，丁}， {丙，丁}共6个， 10分

设“随机抽取两人，这两人的两科成绩均为”为事件，则事件包含的事件有1个，则. 12分

练习册系列答案
相关题目

【题目】已知圆的圆心在直线上，且与直线相切于点，

（1）求圆方程；

（2）是否存在过点的直线与圆交于两点，且的面积是（为坐标原点），若存在，求出直线的方程，若不存在，请说明理由.

【题目】已知抛物线的焦点坐标为.

（1）求抛物线的标准方程；

（2）过点作互相垂直的直线,与抛物线分别相交于两点和两点，求四边形面积的最小值.

【题目】已知函数f（x）的定义域是（0，+∞），且满足f（xy）=f（x）+f（y），当x＞1时，有f（x）＞0．
（1）求f（1），判定并证明f（x）的单调性；
（2）若f（2）=1，解不等式f（﹣x）+f（3﹣x）≥﹣2．

【题目】某学校上学期的期中考试后，为了了解某学科的考试成绩，根据学生的考试成绩利用分层抽样抽取名学生的成绩进行统计（所有学生成绩均不低于分），得到学生成绩的频率分布直方图如图，回答下列问题；

（Ⅰ）根据频率分布直方图计算本次考试成绩的平均分；

（Ⅱ）已知本次全校考试成绩在内的人数为，试确定全校的总人数；

（Ⅲ）若本次考试抽查的人中考试成绩在内的有名女生，其余为男生，从中选择两名学生，求选择一名男生与一名女生的概率.

【题目】已知二次函数f（x）=ax2+bx+1，a，b∈R，当x=﹣1时，函数f（x）取到最小值，且最小值为0；
（1）求f（x）解析式；
（2）关于x的方程f（x）=|x+1|﹣k+3恰有两个不相等的实数解，求实数k的取值范围．

【题目】运货卡车以每小时x千米的速度匀速行驶130千米，按交通法规限制50≤x≤100（单位：千米/时）．假设汽油的价格是每升2元，而汽车每小时耗油升，司机的工资是每小时14元．

（1）求这次行车总费用y关于x的表达式；

（2）当x为何值时，这次行车的总费用最低，并求出最低费用的值．

【题目】为了解某校高三学生的视力情况，随机地抽查了该校100名高三学生的视力情况，得到频率分布直方图如下图，由于不慎将部分数据丢失，但知道前4组的频数成等比数列，后6组的频数成等差数列，设最大频率为a，视力在4.6到5.0之间的学生数为b，则a，b的值分别为 (　 　)

A. 0.27,78 B. 0.27,83 C. 2.7,78 D. 2.7,83

【题目】设函数.

（1）当时，求的单调区间；

（2）当时， 恒成立，求的取值范围；

（3）求证：当时， .

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网