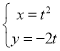题目内容
【题目】已知函数f(x)的定义域是(0,+∞),且满足f(xy)=f(x)+f(y),当x>1时,有f(x)>0.
(1)求f(1),判定并证明f(x)的单调性;
(2)若f(2)=1,解不等式f(﹣x)+f(3﹣x)≥﹣2.
【答案】
(1)解:令x=y=1,则f(1)=f(1)+f(1),解得f(1)=0.
f(x)在(0,+∞)上的是增函数,
设x1,x2∈(0,+∞),且x1>x2,则 ![]() >1,
>1,
∴f( ![]() )>0,
)>0,
∴f(x1)﹣f(x2)=f(x2 ![]() )﹣f(x2)=f(
)﹣f(x2)=f( ![]() )>0,
)>0,
即f(x1)>f(x2),
∴f(x)在(0,+∞)上的是增函数
(2)解:∵f(2)=1,∴f(﹣x)+f(3﹣x)≥﹣2,
可化为f(﹣x)+f(3﹣x)≥﹣2f(2).
∴f(﹣x)+f(2)+f(3﹣x)+f(2)≥0,
∴f(﹣2x)+f(6﹣2x)≥f(1),
∴f[﹣2x(6﹣2x)]≥f(1),
∴ 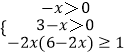 ,
,
∴x≤ ![]() .
.
∴不等式的解集为{x|x≤ ![]() }
}
【解析】(1)利用赋值法进行求f(1)的值; 根据函数的单调性的定义判断f(x)在(0,+∞)上的单调性,并证明.(2)根据函数单调性的性质解不等式即可.
【考点精析】本题主要考查了函数单调性的判断方法的相关知识点,需要掌握单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较才能正确解答此题.

【题目】2017年某市街头开始兴起“mobike”、“ofo”等共享单车,这样的共享单车为很多市民解决了最后一公里的出行难题.然而,这种模式也遇到了一些让人尴尬的问题,比如乱停乱放,或将共享单车占为“私有”等.为此,某机构就是否支持发展共享单车随机调查了50人,他们年龄的分布及支持发展共享单车的人数统计如下表:
年龄 |
|
|
|
|
|
|
受访人数 | 5 | 6 | 15 | 9 | 10 | 5 |
支持发展共享单车人数 | 4 | 5 | 12 | 9 | 7 | 3 |
(Ⅰ)由以上统计数据填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系:
列联表,并判断能否在犯错误的概率不超过0.1的前提下,认为年龄与是否支持发展共享单车有关系:
年龄低于35岁 | 年龄不低于35岁 | 合计 | |
支持 | |||
不支持 | |||
合计 |
(Ⅱ)若对年龄在![]() 的被调查人中随机选取两人,对年龄在
的被调查人中随机选取两人,对年龄在![]() 的被调查人中随机选取一人进行调查,求选中的3人中支持发展共享单车的人数为2人的概率.
的被调查人中随机选取一人进行调查,求选中的3人中支持发展共享单车的人数为2人的概率.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式: 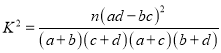 ,其中
,其中![]() .
.