题目内容
18．
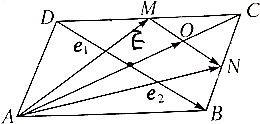已知在?ABCD中，M、N分别是DC、BC的中点，若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$，$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$，试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$．
分析 利用向量加法、减法的三角形法则，即可得出结论．
解答 解：由题意，$\overrightarrow{MN}$=$\overrightarrow{AN}$-$\overrightarrow{AM}$=$\overrightarrow{{e}_{2}}$-$\overrightarrow{{e}_{1}}$，
∵M、N分别是DC、BC的中点，
∴$\overrightarrow{DB}$=2$\overrightarrow{MN}$，
∴$\overrightarrow{DB}$=2$\overrightarrow{{e}_{2}}$-2$\overrightarrow{{e}_{1}}$，
∵?ABCD中，M、N分别是DC、BC的中点，
∴O是MN的中点，
∴$\overrightarrow{AO}$=$\frac{1}{2}$（$\overrightarrow{AN}$-$\overrightarrow{AM}$）=$\frac{1}{2}$（$\overrightarrow{{e}_{2}}$+$\overrightarrow{{e}_{1}}$）．
点评 本题主要考查平面向量基本定理及其几何意义，向量加法的三角形法则的应用，体现了数形结合的数学思想，属于中档题．
练习册系列答案
相关题目
正三棱柱ABC-A1B1C1中，AB=BB1，D是BC的中点．