题目内容
8.已知函数f(x)=ln(1+x)+$\frac{1}{2}$x2-x.(1)证明:x>0,f(x)>0.
(2)证明:ln(1+$\frac{1}{{n}^{2}}$)+ln(1+$\frac{2}{{n}^{2}}$)+…+ln(1+$\frac{k}{{n}^{2}}$)+…+ln(1+$\frac{n}{{n}^{2}}$)>$\frac{1}{2}$(n∈N*);
(3)(1+$\frac{1}{{n}^{2}}$)(1+$\frac{2}{{n}^{2}}$)…(1+$\frac{k}{{n}^{2}}$)…(1+$\frac{n}{{n}^{2}}$)>$\sqrt{e}$.
分析 (1)只需求出函数f(x)的导数,然后求出该函数的最小值,说明最小值大于零即可;
(2)利用第(1)问的结果得到ln(x+1)$>x-\frac{1}{2}{x}^{2}$,然后将不等式中左边的每一个加数缩小,转化为数列求和问题,化简后即可证得结论;
(3)利用第二问结论,容易证得结论.
解答 解:(1)由已知得$f′(x)=\frac{1}{x+1}+x-1=\frac{{x}^{2}}{x+1}$,
因为x>0,所以f′(x)>0恒成立,所以f(x)在(0,+∞)上递增,且当x→0时,f(x)→0.
所以x>0,f(x)>0.
(2)由(1)可知,当x>0时,ln(1+x)$>x-\frac{1}{2}{x}^{2}$.
所以ln(1+$\frac{1}{{n}^{2}}$)+ln(1+$\frac{2}{{n}^{2}}$)+…+ln(1+$\frac{k}{{n}^{2}}$)+…+ln(1+$\frac{n}{{n}^{2}}$)>$\frac{1}{{n}^{2}}+\frac{2}{{n}^{2}}+…+\frac{n}{{n}^{2}}-\frac{1}{2}[\frac{{1}^{2}}{{n}^{4}}+\frac{{2}^{2}}{{n}^{4}}+…+$$\frac{{n}^{2}}{{n}^{4}}]$
=$\frac{\frac{n(n+1)}{2}}{{n}^{2}}-\frac{1}{2}[\frac{\frac{n(n+1)(2n+1)}{6}}{{n}^{4}}]$=$\frac{{n}^{2}+n}{{2n}^{2}}-\frac{1}{2}×\frac{\frac{2{n}^{3}+3{n}^{2}+n}{6}}{{n}^{4}}$=$\frac{1}{2}[1+\frac{{n}^{3}-\frac{2{n}^{3}+3{n}^{2}+n}{6}}{{n}^{4}}]$
=$\frac{1}{2}[1+\frac{\frac{4{n}^{3}-3{n}^{2}-n}{6}}{{n}^{4}}]=\frac{1}{2}(1+\frac{n(n-1)(4n+1)}{6{n}^{4}})$.显然n(n-1)(4n+1)≥0.
故$\frac{1}{2}(1+\frac{n(n-1)(2n+1)}{6{n}^{4}})≥\frac{1}{2}$.
故ln(1+$\frac{1}{{n}^{2}}$)+ln(1+$\frac{2}{{n}^{2}}$)+…+ln(1+$\frac{k}{{n}^{2}}$)+…+ln(1+$\frac{n}{{n}^{2}}$)>$\frac{1}{2}$对任意的n∈N*成立.
(3)由(2)知ln(1+$\frac{1}{{n}^{2}}$)+ln(1+$\frac{2}{{n}^{2}}$)+…+ln(1+$\frac{k}{{n}^{2}}$)+…+ln(1+$\frac{n}{{n}^{2}}$)>$\frac{1}{2}$成立.
故ln[$(1+\frac{1}{{n}^{2}})(1+\frac{2}{{n}^{2}})×…×(1+\frac{n}{{n}^{2}})$]$>ln\sqrt{e}$.
由函数y=lnx在定义域内是增函数得:(1+$\frac{1}{{n}^{2}}$)(1+$\frac{2}{{n}^{2}}$)…(1+$\frac{k}{{n}^{2}}$)…(1+$\frac{n}{{n}^{2}}$)>$\sqrt{e}$.
点评 本题考查了导数在研究函数的单调性中的应用,以及利用放缩法结合函数的性质证明不等式问题的思路,属于有些技巧的类型,要仔细体会.

| A. | $(\begin{array}{l}{0}\\{0}\end{array})$ | B. | $(\begin{array}{l}{0}\\{1}\end{array})$ | C. | $(\begin{array}{l}{1}\\{0}\end{array})$ | D. | $(\begin{array}{l}{1}\\{1}\end{array})$ |
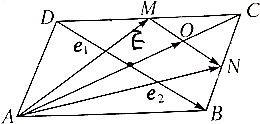 已知在?ABCD中,M、N分别是DC、BC的中点,若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$,试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$.
已知在?ABCD中,M、N分别是DC、BC的中点,若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$,试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$.