题目内容
6．如果不等式$\frac{x-a}{{x}^{2}+x+1}$＞$\frac{x-b}{{x}^{2}-x+1}$的解集为（$\frac{1}{2}$，1），则a•b=8．分析 根据不等式和方程之间的关系建立方程即可．
解答 解：∵不等式$\frac{x-a}{{x}^{2}+x+1}$＞$\frac{x-b}{{x}^{2}-x+1}$的解集为（$\frac{1}{2}$，1），
∴x=$\frac{1}{2}$，1是方程$\frac{x-a}{{x}^{2}+x+1}$=$\frac{x-b}{{x}^{2}-x+1}$的两个根，
则$\left\{\begin{array}{l}{\frac{1-a}{1+1+1}=\frac{1-b}{1-1+1}}\\{\frac{\frac{1}{2}-a}{\frac{1}{4}+\frac{1}{2}+1}=\frac{\frac{1}{2}-b}{\frac{1}{4}-\frac{1}{2}+1}}\end{array}\right.$，
即$\left\{\begin{array}{l}{\frac{1-a}{3}=1-b}\\{\frac{1-2a}{7}=\frac{1-2b}{3}}\end{array}\right.$，解得a=4，b=2，
则ab=2×4=8，
故答案为：8．
点评 本题主要考查不等式的应用，根据不等式的解和方程根之间的关系是解决本题的关键．
练习册系列答案
相关题目
16．在平面直角坐标系xOy中，椭圆$\frac{x{\;}^{2}}{a{\;}^{2}}$+$\frac{y{\;}^{2}}{b{\;}^{2}}$=1（a＞b＞0）内接四边形ABCD（点A、B、C、D在椭圆上）的对角线AC、BD相交于P（$\frac{1}{b{\;}^{2}}$，$\frac{1}{a{\;}^{2}}$），且$\overrightarrow{AP}$=λ$\overrightarrow{PC}$，$\overrightarrow{BP}$=λ$\overrightarrow{PD}$，则直线AB的斜率为（ ）
| A． | $\frac{-a{\;}^{2}-c{\;}^{2}}{c{\;}^{2}}$ | B． | $\frac{c（λ-1）}{a}$ | C． | -1 | D． | -2 |
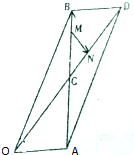如图，平行四边形OADB的对角线OD、AB相交于点C，线段BC上有一点M满足BC=3BM，线段CD上有一点N满足CD=3CN，设|$\overrightarrow{OA}$|=2，|$\overrightarrow{OB}$|=6，∠AOB=60°．
11．指数方程22x+1-9•2x+4=0的解集是（ ）
| A． | {2} | B． | {-1} | C． | {$\frac{1}{2}$} | D． | {-1，2} |
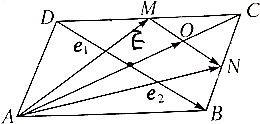已知在?ABCD中，M、N分别是DC、BC的中点，若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$，$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$，试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$．