题目内容
1. 正三棱柱ABC-A1B1C1中,AB=BB1,D是BC的中点.
正三棱柱ABC-A1B1C1中,AB=BB1,D是BC的中点.(1)求直线BB1与平面AC1D所成的余弦值;
(2)求二面角A1-AC1-D.
分析 (1)先证明平面ADBC1⊥平面CBB1C1,过C作CE⊥C1D,说明CC1E是BB1与平面AC1D所成角,通过三角形相似解三角形从而可求BB1与平面CDB1所成角的余弦值.
(2)分别求出平面AC1D的法向量和平面AC1C的法向量,代入向量夹角公式,即可求出二面角C-AC1-D的余弦值,进而得到二面角A1-AC1-D的大小.
解答  (1)解:∵正三棱柱ABC-A1B1C1中,D点为棱BC的中点.
(1)解:∵正三棱柱ABC-A1B1C1中,D点为棱BC的中点.
∴AD⊥平面CBB1C1,
∵AD?平面CDC1.
∴平面ADBC1⊥平面CBB1C1,
过C作CE⊥C1D,∵平面ADC1∩CBB1C1=C1D
∴CE⊥平面ADC1.
∴∠CC1E是BB1与平面AC1D所成角
∵CC1⊥BC
∴△CEC1∽△DCC1,
由CD=$\frac{1}{2}$BC=1,CC1=2
C1D=$\sqrt{5}$
得cos∠CC1E=$\frac{\sqrt{5}}{2}$.
即直线BB1与平面AC1D所成的余弦值:$\frac{\sqrt{5}}{2}$.
(2)取B1C1的中点D1,以D点为坐标原点,以DD1所在直线为z轴,
以DA所在直线为x轴,所在DC所在直线为y轴建立空间直角坐标系,AA1=2,
则D(0,0,0),C(0,1,0),A($\sqrt{3}$,0,0),M(0,-1,1),C1(0,1,2),
设平面AC1D的法向量为$\overrightarrow{n}$=(x,y,z),$\left\{\begin{array}{l}\overrightarrow{n}•\overrightarrow{AD}=0\\ \overrightarrow{n}•\overrightarrow{{DC}_{1}}=0\end{array}\right.$,$\left\{\begin{array}{l}-\sqrt{3}x=0\\ y+2z=0\end{array}\right.$,令z=1,则y=-2,
可求得$\overrightarrow{n}$=(0,-2,1),
设平面AC1C的法向量为$\overrightarrow{m}$,
可求得$\overrightarrow{m}$=(1,$\sqrt{3}$,0),
cos<$\overrightarrow{n}$,$\overrightarrow{m}$>=$\frac{\sqrt{15}}{5}$;
∴二面角C-AC1-D的大小为:π-arccos$\frac{\sqrt{15}}{5}$.
点评 本题考查的知识点是用空间向量求平面间的夹角,直线与平面垂直的判定,其中解答本题的关键是建立空间坐标系,将线面平行问题和二面角问题转化为向量垂直及向量夹角问题.

| A. | {2} | B. | {-1} | C. | {$\frac{1}{2}$} | D. | {-1,2} |
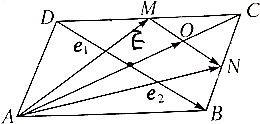 已知在?ABCD中,M、N分别是DC、BC的中点,若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$,试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$.
已知在?ABCD中,M、N分别是DC、BC的中点,若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$,试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$.