题目内容
5.△ABC中,已知cosC=-$\frac{3}{5}$,sinB=$\frac{5}{13}$,则sinA=$\frac{33}{65}$.分析 根据两角和差的正弦公式进行求解即可.
解答 解:在△ABC中,已知cosC=-$\frac{3}{5}$,sinB=$\frac{5}{13}$,
则$\frac{π}{2}$<C<π,则0<B<$\frac{π}{2}$,
则sinC=$\frac{4}{5}$,cosB=$\frac{12}{13}$,
则sinA=sin[π-(B+C)]=sin(B+C)=sinBcosC+cosBsinC=$\frac{5}{13}$×(-$\frac{3}{5}$)+$\frac{4}{5}$×$\frac{12}{13}$=$\frac{33}{65}$,
故答案为:$\frac{33}{65}$.
点评 本题主要考查三角函数值的计算,根据两角和差的正弦公式是解决本题的关键.

练习册系列答案
相关题目
20.定义运算$(\begin{array}{l}{a}&{b}\\{c}&{d}\end{array})$•$(\begin{array}{l}{e}\\{f}\end{array})$=$(\begin{array}{l}{ae+bf}\\{ce+df}\end{array})$,如$(\begin{array}{l}{1}&{2}\\{0}&{3}\end{array})$•$(\begin{array}{l}{4}\\{5}\end{array})$=$(\begin{array}{l}{14}\\{15}\end{array})$.已知α+β=π,α-β=$\frac{π}{2}$,则$(\begin{array}{l}{sinα}&{cosα}\\{cosα}&{sinα}\end{array})$•$(\begin{array}{l}{cosβ}\\{sinβ}\end{array})$=( )
| A. | $(\begin{array}{l}{0}\\{0}\end{array})$ | B. | $(\begin{array}{l}{0}\\{1}\end{array})$ | C. | $(\begin{array}{l}{1}\\{0}\end{array})$ | D. | $(\begin{array}{l}{1}\\{1}\end{array})$ |
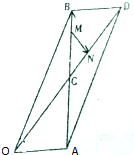 如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=6,∠AOB=60°.
如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=6,∠AOB=60°.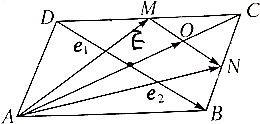 已知在?ABCD中,M、N分别是DC、BC的中点,若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$,试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$.
已知在?ABCD中,M、N分别是DC、BC的中点,若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$,试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$.