题目内容
9.设随机变量ξ~B(2,P),η=2ξ-1,若P(η≥1)=$\frac{65}{81}$,则E(ξ)=$\frac{10}{9}$.分析 由已知得P(ξ=1)+P(ξ=2)=${C}_{2}^{1}p(1-p)+{C}_{2}^{2}{p}^{2}$=$\frac{65}{81}$,解得p,能求出Eξ.
解答 解:∵η=2ξ-1,P(η≥1)=$\frac{65}{81}$,∴P(ξ≥1)=$\frac{65}{81}$,
∵随机变量ξ~B(2,p),
∴P(ξ=1)+P(ξ=2)=${C}_{2}^{1}p(1-p)+{C}_{2}^{2}{p}^{2}$=$\frac{65}{81}$,
解得p=$\frac{5}{9}$或p=$\frac{13}{9}$(舍),
∴E(ξ)=$\frac{10}{9}$.
故答案为:$\frac{10}{9}$.
点评 本题考查离散型随机变量的数学期望的求法,解题时要认真审题,注意二项分布的合理运用,是中档题.

练习册系列答案
相关题目
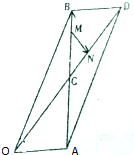 如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=6,∠AOB=60°.
如图,平行四边形OADB的对角线OD、AB相交于点C,线段BC上有一点M满足BC=3BM,线段CD上有一点N满足CD=3CN,设|$\overrightarrow{OA}$|=2,|$\overrightarrow{OB}$|=6,∠AOB=60°. 如图,已知正三棱柱ABC-A1B1C1的各棱长均为4,E是BC的中点,点F在侧棱CC1上,且CC1=4CF
如图,已知正三棱柱ABC-A1B1C1的各棱长均为4,E是BC的中点,点F在侧棱CC1上,且CC1=4CF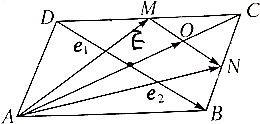 已知在?ABCD中,M、N分别是DC、BC的中点,若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$,试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$.
已知在?ABCD中,M、N分别是DC、BC的中点,若$\overrightarrow{AM}$=$\overrightarrow{{e}_{1}}$,$\overrightarrow{AN}$=$\overrightarrow{{e}_{2}}$,试用$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$表示$\overrightarrow{DB}$、$\overrightarrow{AO}$.