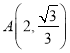题目内容
【题目】在平面直角坐标系中,![]() 为坐标原点.对任意的点
为坐标原点.对任意的点![]() ,定义
,定义![]() .任取点
.任取点![]() ,
,![]() ,记
,记![]() ,
,![]() ,若此时
,若此时![]() 成立,则称点
成立,则称点![]() ,
,![]() 相关.
相关.
(1)分别判断下面各组中两点是否相关,并说明理由;
①![]() ,
,![]() ;②
;②![]() ,
,![]() .
.
(2)给定![]() ,
,![]() ,点集
,点集![]() .
.
(![]() )求集合
)求集合![]() 中与点
中与点![]() 相关的点的个数;
相关的点的个数;
(![]() )若
)若![]() ,且对于任意的
,且对于任意的![]() ,
,![]() ,点
,点![]() ,
,![]() 相关,求
相关,求![]() 中元素个数的最大值.
中元素个数的最大值.
【答案】(1)①相关;②不相关.(2)(![]() )
)![]() 个(
个(![]() )
)![]() .
.
【解析】
(1)根据所给定义,代入不等式化简变形可得对应坐标满足的关系,即可判断所给两个点的坐标是否符合定义要求.
(2)(![]() )根据所给点集,依次判断在四个象限内满足的点个数,坐标轴上及原点的个数,即可求得集合
)根据所给点集,依次判断在四个象限内满足的点个数,坐标轴上及原点的个数,即可求得集合![]() 中与点
中与点![]() 相关的点的个数;(
相关的点的个数;(![]() )由(1)可知相关点满足
)由(1)可知相关点满足![]() ,利用分类讨论证明
,利用分类讨论证明![]() ,即可求得
,即可求得![]() 中元素个数的最大值.
中元素个数的最大值.
若点![]() ,
,![]() 相关,则
相关,则![]() ,
,![]() ,而
,而![]() ,
,
不妨设![]() ,
,
则由定义![]() 可知
可知![]() ,
,
化简变形可得![]() ,
,
(1)对于①![]() ,
,![]() ;对应坐标取绝对值,代入可知
;对应坐标取绝对值,代入可知![]() 成立,因此相关;
成立,因此相关;
②对应坐标取绝对值,代入可知![]() ,因此不相关.
,因此不相关.
(2)(![]() )在第一象限内,
)在第一象限内,![]() ,可知
,可知![]() 且
且![]() ,有
,有![]() 个点;同理可知,在第二象限、第三象限、第四象限也各有
个点;同理可知,在第二象限、第三象限、第四象限也各有![]() 个点.
个点.
在![]() 轴正半轴上,点
轴正半轴上,点![]() 满足条件;在
满足条件;在![]() 轴负半轴上,点
轴负半轴上,点![]() 满足条件;
满足条件;
在![]() 轴正半轴上,点
轴正半轴上,点![]() 满足条件;在
满足条件;在![]() 轴负半轴上,点
轴负半轴上,点![]() 满足条件;
满足条件;
原点![]() 满足条件;
满足条件;
因此集合![]() 中共有
中共有![]() 个点与点
个点与点![]() 相关.
相关.
(![]() )若两个不同的点
)若两个不同的点![]() ,
,![]() 相关,其中
相关,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可知![]() .
.
下面证明![]() .
.
若![]() ,则
,则![]() ,成立;
,成立;
若![]() ,则
,则![]() ,
,
若![]() ,则
,则![]() ,亦成立.
,亦成立.
由于![]() ,
,
因此最多有![]() 个点两两相关,其中最多有
个点两两相关,其中最多有![]() 个点在第一象限;最少有1个点在坐标轴正半轴上,一个点为原点.
个点在第一象限;最少有1个点在坐标轴正半轴上,一个点为原点.
因此![]() 中元素个数的最大值为
中元素个数的最大值为![]() .
.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目