题目内容
16.在如图的平面多边形ACBEF中,四边形ABEF是矩形,点O为AB的中点,△ABC中,AC=BC,现沿着AB将△ABC折起,直至平面ABEF⊥平面ABC,如图,此时OE⊥FC.(1)求证:OF⊥EC;
(2)若FC与平面ABC所成角为30°,求二面角F-CE-B的余弦值.

分析 (Ⅰ)连结OC,则OC⊥AB,从而得到OC⊥OE,进而得到OF⊥OE,由此能证明OF⊥EC.
(Ⅱ)由(I)得AB=2AF.设AF=1,AB=2.由∠FCA为直线FC与平面ABC所成的角,知∠FCA=30°,由已知条件推导出∠FMP为二面角F-CE-B的平面角,由此能求出二面角F-CE-B的余弦值
解答 (Ⅰ)证明:连结OC,∵AC=BC,O是AB的中点,故OC⊥AB. 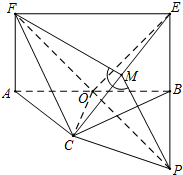
又∵平面ABC⊥平面ABEF,
故OC⊥平面ABE,
于是OC⊥OF.OC⊥OE,
又OE⊥FC,
∵OF⊥平面OFC,
∴OE⊥OF,
又∵OC⊥OF,∴OF⊥平面OEC,
∴OF⊥EC.
(Ⅱ)由(I)得AB=2AF.不妨设AF=1,AB=2.
∵∠FCA为直线FC与平面ABC所成的角,
∴∠FCA=30°,
∴FC=EC=2,△EFC为等边三角形.
设FO∩EB=P,则O,B分别为PF,PE的中点,△PEC也是等边三角形.
取EC的中点M,连结FM,MP,则FM⊥CE,MP⊥CE,
∴∠FMP为二面角F-CE-B的平面角.
在△MFP中,FM=MP=$\sqrt{3}$,FP=2$\sqrt{2}$,
故cos∠FMP=$\frac{F{M}^{2}+M{P}^{2}-F{P}^{2}}{2FM•MP}$=$\frac{3+3-8}{3×\sqrt{3}×\sqrt{3}}$=$-\frac{1}{3}$,
即二面角F-CE-B的余弦值为-$\frac{1}{3}$.
点评 本题考查异面直线垂直的证明,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养,本题也可以建立坐标系,利用向量法进行求解.

练习册系列答案
相关题目
6.若x,y满足约束条件$\left\{\begin{array}{l}{x+y≥2}\\{y≤2}\\{x≤2y}\end{array}\right.$则目标函数z=x2+y2的最小值为( )
| A. | $\frac{20}{9}$ | B. | 2 | C. | 3 | D. | 4 |
8.在平面直角坐标系中,不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y-8≤0}\end{array}\right.$所表示的平面区域是α,不等式组$\left\{\begin{array}{l}0≤x≤4\\ 0≤y≤10\end{array}\right.$所表示的平面区域为α,在区域α内随机取一点P,则点P落在区域β内的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{5}$ | D. | $\frac{3}{4}$ |
3.某市为了治理污染,改善空气质量,市环境保护局决定每天在城区主要路段洒水防尘,为了给洒水车供水,供水部门决定最多修建3处供水站.根据过去30个月的资料显示,每月洒水量X(单位:百立方米)与气温和降雨量有关,且每月的洒水量都在20以上,其中不足40的月份有10个月,不低于40且不超过60的月份有15个月,超过60的月份有5个月.将月洒水量在以上三段的频率作为相应的概率,并假设各月的洒水量相互独立.
(Ⅰ)求未来的3个月中,至多有1个月的洒水量超过60的概率;
(Ⅱ)供水部门希望修建的供水站尽可能运行,但每月供水站运行的数量受月洒水量限制,有如下关系:
若某供水站运行,月利润为12000元;若某供水站不运行,月亏损6000元.欲使供水站的月总利润的均值最大,应修建几处供水站?
(Ⅰ)求未来的3个月中,至多有1个月的洒水量超过60的概率;
(Ⅱ)供水部门希望修建的供水站尽可能运行,但每月供水站运行的数量受月洒水量限制,有如下关系:
| 月洒水量 | 20<X<40 | 40≤X≤60 | X>60 |
| 供水站运行的最多数量 | 1 | 2 | 3 |