题目内容
5．已知不等式组$\left\{\begin{array}{l}{m+n≤2}\\{n-m≤2}\\{n≥1}\end{array}\right.$，求$\sqrt{{m}^{2}+{n}^{2}}$的取值范围．分析 由题意作出可行域，由$\sqrt{{m}^{2}+{n}^{2}}$的几何意义即可求得其取值范围．
解答 解：由约束条件$\left\{\begin{array}{l}{m+n≤2}\\{n-m≤2}\\{n≥1}\end{array}\right.$作出可行域如图，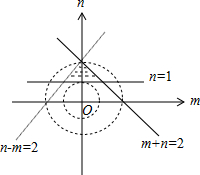
$\sqrt{{m}^{2}+{n}^{2}}$的几何意义为坐标原点到可行域内动点距离，
由图可知：$（\sqrt{{m}^{2}+{n}^{2}}）_{min}=1，（\sqrt{{m}^{2}+{n}^{2}}）max=2$．
∴$\sqrt{{m}^{2}+{n}^{2}}$的取值范围是（1，2）．
点评 本题考查了简单的线性规划，考查了数形结合的解题思想方法，是中档题．
练习册系列答案
相关题目
15．某中学有三个年级，各年级男、女生人数如表所示：
已知在全校学生中随机抽取1名学生，抽到三年级男生的概率是0.15．
（Ⅰ）求z的值；
（Ⅱ）用水机抽样的方法从高一年级女生中选出8人，测量他们的体重，结果如下：52，56，60，61，55，62，58，59（单位：kg）．把这8人的体重看作一个总体，从中任取一个数，求该数ξ样本平均数之差的绝对值不超过2的概率；
（Ⅲ）用分层抽样的方法在高三年级中抽取一个容量为5的样本，将该样本看成一个总体，从中任选2名学生，求这2名学生均为男生的概率．
| 高一年级 | 高二年级 | 高三年级 | |
| 女生 | 370 | z | 200 |
| 男生 | 380 | 370 | 300 |
（Ⅰ）求z的值；
（Ⅱ）用水机抽样的方法从高一年级女生中选出8人，测量他们的体重，结果如下：52，56，60，61，55，62，58，59（单位：kg）．把这8人的体重看作一个总体，从中任取一个数，求该数ξ样本平均数之差的绝对值不超过2的概率；
（Ⅲ）用分层抽样的方法在高三年级中抽取一个容量为5的样本，将该样本看成一个总体，从中任选2名学生，求这2名学生均为男生的概率．
已知点P（c，$\frac{3}{2}$c）在以F（c，0）为右焦点的椭圆Γ：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）上，斜率为l的直线m过点F与椭圆Γ交于A，B两点，且与直线l：x=4c交于点M，求椭圆Γ的离心率e．