题目内容
17.过抛物线y2=2px(p>0)的焦点F作倾斜角为135°的直线,交抛物线于A,B两点,则△OAB的面积为( )| A. | $\frac{{\sqrt{2}}}{2}{p^2}$ | B. | $\sqrt{2}{p^2}$ | C. | p2 | D. | 2p2 |
分析 写出过A,B两点的直线方程,和抛物线方程联立后化为关于y的一元二次方程,由根与系数关系得到A,B两点纵坐标的和与积,把△OAB的面积表示为两个小三角形AOF与BOF的面积和得答案.
解答 解:弦AB的方程y=-x+$\frac{p}{2}$,把它与y2=2px联立得关于y的一元二次方程y2+2py-p2=0,
设A(x1,y1),B(x2,y2),
则y1+y2=-2p,y1y2=-p2.
∴S△OAB=S△OAF+S△OFB=$\frac{p}{4}$|y1-y2|=$\frac{p}{4}$×$\sqrt{4{p}^{2}+4{p}^{2}}$=$\frac{\sqrt{2}}{2}{p}^{2}$
故选:A.
点评 本题考查直线与抛物线的位置关系,考查数学转化思想方法,涉及直线和圆锥曲线关系问题,常采用联立直线和圆锥曲线,然后利用一元二次方程的根与系数关系解题,是中档题.

练习册系列答案
相关题目
12.在△ABC中,若∠B=30°,AB=2$\sqrt{3}$,AC=2,则△ABC的面积为( )
| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$或$\sqrt{2}$ | C. | 2$\sqrt{3}$或$\sqrt{3}$ | D. | 2$\sqrt{3}$ |
2.已知α∈(0,$\frac{π}{2}$),三个数sinα+$\frac{4}{cosα}$,cosα+$\frac{4}{tanα}$,tanα+$\frac{4}{sinα}$中( )
| A. | 都小于$\frac{14}{3}$ | B. | 至少一个大于或等于$\frac{14}{3}$ | ||
| C. | 都大于或等于4 | D. | 至多一个大于5 |
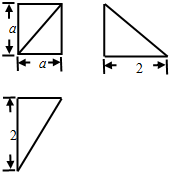 如图是一个几何体的三视图,若它的体积是$\frac{2}{3}$,则a=1,该几何体的表面积为$3+\sqrt{5}$.
如图是一个几何体的三视图,若它的体积是$\frac{2}{3}$,则a=1,该几何体的表面积为$3+\sqrt{5}$.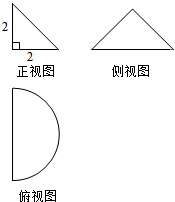 一个几何体的正视图、侧视图、俯视图如图所示,则该几何体的表面积为4+2π+2$\sqrt{2}$π.体积分别为$\frac{4}{3}$π.
一个几何体的正视图、侧视图、俯视图如图所示,则该几何体的表面积为4+2π+2$\sqrt{2}$π.体积分别为$\frac{4}{3}$π.