题目内容
9．
如图是一个几何体的三视图，若它的体积是$\frac{2}{3}$，则a=1，该几何体的表面积为$3+\sqrt{5}$．
分析 由已知中的三视图，可知该几何体是一个以主视图为底面的四棱锥，根据它的体积是$\frac{2}{3}$，求出a值，再计算各个面的面积，相加可得答案．
解答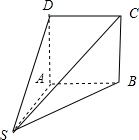 
解：由已知中的三视图，可知该几何体是一个以主视图为底面的四棱锥，
其直观图如图所示：
其底面面积S=a2，高SA=2，
故它的体积V=$\frac{1}{3}S•SA$=$\frac{2}{3}{a}^{2}$=$\frac{2}{3}$，
解得：a=1，
则底面面积S=1，
侧面S△SAD=S△SAB=$\frac{1}{2}×2×1=1$，
侧面S△SCD=S△SCB=$\frac{1}{2}×\sqrt{5}×1=1$=$\frac{\sqrt{5}}{2}$，
故几何体的表面积为：1+2×1+2×$\frac{\sqrt{5}}{2}$=$3+\sqrt{5}$，
故答案为：1；$3+\sqrt{5}$
点评 本题考查的知识点是由三视图求体积和表面积，解决本题的关键是得到该几何体的形状．
练习册系列答案
相关题目
17．过抛物线y2=2px（p＞0）的焦点F作倾斜角为135°的直线，交抛物线于A，B两点，则△OAB的面积为（ ）
| A． | $\frac{{\sqrt{2}}}{2}{p^2}$ | B． | $\sqrt{2}{p^2}$ | C． | p2 | D． | 2p2 |
4．“孝敬父母．感恩社会”是中华民族的传统美德．从出生开始，父母就对们关心无微不至，其中对我们物质帮助是最重要的一个指标，下表是一个统计员在统计《父母为我花了多少》当中使用处理得到下列的数据：
参考数据公式：$\sum_{i=1}^6{x_i}{y_i}$=1024.6，$\sum_{i=1}^6{{x_i}^2}$=730，
线性回归方程：$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，（$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{n=i}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$）
假设花费累积y与岁数x符合线性相关关系，求
（1）花费累积y与岁数x的线性回归直线方程（系数保留3位小数）；
（2）24岁大学毕业之后，我们不再花父母的钱，假设你在30岁成家立业之后，在你50岁之前偿还父母为你的花费（不计利息）．那么你每月要偿还父母约多少元钱？
参考数据公式：$\sum_{i=1}^6{x_i}{y_i}$=1024.6，$\sum_{i=1}^6{{x_i}^2}$=730，
线性回归方程：$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，（$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{xy}}{\sum_{n=i}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$）
| 岁数x | 1 | 2 | 6 | 12 | 16 | 17 |
| 花费累积y（万元） | 1 | 2.8 | 9 | 17 | 22 | 24 |
（1）花费累积y与岁数x的线性回归直线方程（系数保留3位小数）；
（2）24岁大学毕业之后，我们不再花父母的钱，假设你在30岁成家立业之后，在你50岁之前偿还父母为你的花费（不计利息）．那么你每月要偿还父母约多少元钱？