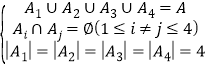题目内容
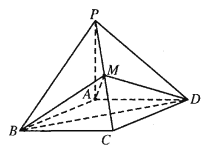
【题目】如图,四棱锥![]() 的底面
的底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() 平面
平面![]() ,点
,点![]() 是棱
是棱![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)当![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
(1)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,则
,则![]() ,
,![]() 分别为
分别为![]() ,
,![]() 中点,由三角形中位线定理可得
中点,由三角形中位线定理可得![]() ,从而可得结论;(2)取线段
,从而可得结论;(2)取线段![]() 的中点
的中点![]() ,先证明
,先证明![]() 垂直于平面
垂直于平面![]() ,则点
,则点![]() 到平面
到平面![]() 的距离即为
的距离即为![]() 的长度. 结合
的长度. 结合![]() A
A![]() ,可得点
,可得点![]() 到平面
到平面![]() 的距离即为
的距离即为![]() 的长度. 由
的长度. 由![]() 为
为![]() 的中点,可得点
的中点,可得点![]() 到平面
到平面![]() 的距离即为
的距离即为![]() 的长度,利用
的长度,利用![]() 即可得结果.
即可得结果.
(1)如图,
连接AC交BD于点O,连接MO.
∵M,O分别为PC,AC中点,
∴PA∥MO ,
∵PA不在平面BMD内,MO![]() 平面BMD.
平面BMD.
∴PA∥平面BMD.
(2)如图,取线段BC的中点H,连结AH.
∵ABCD是菱形,![]() ,∴AH⊥AD.
,∴AH⊥AD.
∵PA⊥平面ABCD,∴AH⊥PA.
又PA∩AD=A,PA,AD![]() 平面PAD.
平面PAD.
AH⊥平面PAD.∴点H到平面PAD的距离即为AH的长度.
∴BC∥AD,∴点C到平面PAD的距离即为AH的长度.
∵M为PC的中点,∴点M到平面PAD的距离即为![]() AH的长度.
AH的长度.

![]() .
.

练习册系列答案
相关题目