题目内容
【题目】正方体ABCD-A1B1C1D1中，E为AB中点，F为CD1中点．
（1）求证：EF∥平面ADD1A1；
（2）求直线EF和平面CDD1C1所成角的正弦值．
【答案】（1）见解析；（2）
【解析】试题分析：（1）取DD1中点M，连接MA，MF，易得AEFM是平行四边形，有EF∥AM，从而得证；
（2）因为EF∥AM，AD⊥平面CDD1C1，所以∠AMD与直线EF和平面CDD1C1所成角相等，在Rt△AMD中求解即可.
试题解析：
（1）证明：取DD1中点M，连接MA，MF，有
，
所以AEFM是平行四边形，
所以EF∥AM，又AM平面ADD1A1，EF平面ADD1A1，
所以EF∥平面ADD1A1，得证．
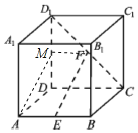
（2）因为EF∥AM，AD⊥平面CDD1C1，所以∠AMD与直线EF和平面CDD1C1所成角相等，
又在Rt△AMD中，有
，所以直线EF和平面CDD1C1所成角的正弦值为
．
【题目】假设某种设备使用的年限x（年）与所支出的维修费用y（万元）有以下统计资料：
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2 | 4 | 5 | 6 | 7 |
若由资料知y对x呈线性相关关系。试求：
（1）求
； （2）线性回归方程
；
（3）估计使用10年时，维修费用是多少？
附：利用“最小二乘法”计算a,b的值时,可根据以下公式：
【题目】某公司即将推车一款新型智能手机，为了更好地对产品进行宣传，需预估市民购买该款手机是否与年龄有关，现随机抽取了50名市民进行购买意愿的问卷调查，若得分低于60分，说明购买意愿弱；若得分不低于60分，说明购买意愿强，调查结果用茎叶图表示如图所示.
（1）根据茎叶图中的数据完成
列联表，并判断是否有95%的把握认为市民是否购买该款手机与年龄有关？
购买意愿强 | 购买意愿弱 | 合计 | |
20~40岁 | |||
大于40岁 | |||
合计 |
（2）从购买意愿弱的市民中按年龄进行分层抽样，共抽取5人，从这5人中随机抽取2人进行采访，求这2人都是年龄大于40岁的概率.
附：
.
