题目内容
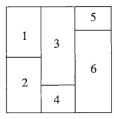
【题目】现用4种不同的颜色对如图所示的正方形的6个区域进行涂色,要求相邻的区域不能涂同一种颜色,则不同的涂色方案有______种.
【答案】144
【解析】
依次计算每个区域的涂色方法种数,然后利用分步乘法计数原理求解即可.
第一步,对区域1进行涂色,有4种颜色可供选择,即有4种不同的涂色方法;
第二步,对区域2进行涂色,区域2与区域1相邻,有3种颜色可供选择,即有3种不同的涂色方法;
第三步,对区域3进行涂色,区域3与区域1、区域2相邻,有2种颜色可供选择,即有2种不同的涂色方法;
第四步,对于区域4进行涂色,区域4与区域2、区域3相邻,有2种颜色可供选择,即有2种不同的涂色方法;
第五步,对区域5进行涂色,若其颜色与区域4相同,则区域6有2种涂色方法,若其颜色与区域4不同,则区域6只有1种涂色方法,故区域5,6共有![]() 种涂色方法,
种涂色方法,
由分步乘法计数原理知,不同的涂色方案的种数为![]() .
.
故答案为:144

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目