题目内容

4．△ABC中，C=60°，a，b边的长是方程x2-8x+6=0的根，则c边长为4$\sqrt{3}$．

分析 根据题意，由a，b边的长是方程x2-8x+6=0的根可得a+b=8，ab=6，而又由由余弦定理可得c2=a2+b2-2abcosC=（a+b）2-2ab-2abcosC，将a+b=8，ab=6代入即可得答案．

解答 解：根据题意，a，b边的长是方程x2-8x+6=0的根，则有a+b=8，ab=6，
由余弦定理可得c2=a2+b2-2abcosC=（a+b）2-2ab-2abcosC
=64-2×6-6=48；
则c=4$\sqrt{3}$；
故答案为：4$\sqrt{3}$．

点评 本题考查余弦定理的运用，涉及一元二次函数的根与系数的关系，注意利用a2+b2=（a+b）2-2ab结合根与系数的关系进行分析．

练习册系列答案
相关题目
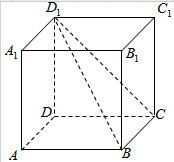14．如图，在正方体ABCD-A1B1C1D1中，找出二面角D1-BC-D的平面角．
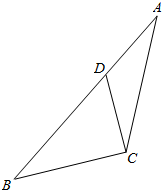15．如图，在△ABC中，已知点D在AB边上，且$\overrightarrow{CB}$•$\overrightarrow{CD}$=0，sin∠ACB=$\frac{5\sqrt{7}}{14}$，AC=$\sqrt{7}$，AD=1．
（Ⅰ）求CD的长；
（Ⅱ）求角B的大小．
12．在平面直角坐标系中，点M是由不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≥4}\end{array}\right.$，所确定的平面区域内的动点，N是圆x2+y2=1上任意一点，0为坐标原点，则|$\overrightarrow{OM}$+$\overrightarrow{ON}$|的最小值为2$\sqrt{2}$-1．
19．己知椭圆的对称中心为原点O，焦点在x轴上，椭圆上异于长轴顶点的任意点A与左右两焦点F1，F2 构成的三角形中面积的最大值为$\sqrt{3}$，且点（$\sqrt{3}$，$\frac{\sqrt{3}}{2}$）在该椭圆上．
（1）求椭圆的方程：
（2）已知点A，B是椭圆上的两动点，若OA⊥OB时，求|AB|的最小值．
9．判断下列函数的奇偶性：
（1）f（x）=5x+1；     
（2）f（x）=-$\frac{2}{{x}^{2}}$+1．
1．在Rt△ABC中，点D是斜边AB上的点，且满足∠ACD=60°，∠BCD=30°，设AC=x，BC=y，DC=2，则x，y满足的相等关系式是y=$\frac{\sqrt{3}x}{x-1}$，（x＞1，y＞$\sqrt{3}$），△ABC面积的最小值是2$\sqrt{3}$．
18．经过点C（4，0），且倾斜角是$\frac{3π}{4}$的直线的极坐标方程是ρcosθ+ρsinθ-4=0．
19．经过直线$l：x+y-2\sqrt{2}=0$上的点P，向圆O：x2+y2=1引切线，切点为A，则切线长|PA|的最小值为（　　）
A．$\sqrt{2}$B．$2\sqrt{2}$C．$\sqrt{3}$D．$2\sqrt{3}$

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网