题目内容
12.在平面直角坐标系中,点M是由不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≥4}\end{array}\right.$,所确定的平面区域内的动点,N是圆x2+y2=1上任意一点,0为坐标原点,则|$\overrightarrow{OM}$+$\overrightarrow{ON}$|的最小值为2$\sqrt{2}$-1.分析 作出平面区域,结合向量的知识和点到直线的距离公式可得.
解答 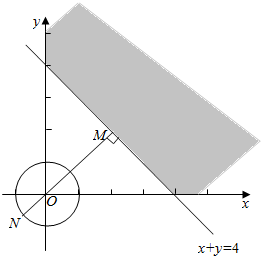 解:不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≥4}\end{array}\right.$表示的区域如图阴影,
解:不等式组$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{x+y≥4}\end{array}\right.$表示的区域如图阴影,
当M、N分别在图中的位置时,|$\overrightarrow{OM}$+$\overrightarrow{ON}$|取最小值,
由点到直线的距离公式可得|OM|=$\frac{4}{\sqrt{{1}^{2}+{1}^{2}}}$=2$\sqrt{2}$,
∴|$\overrightarrow{OM}$+$\overrightarrow{ON}$|的最小值为2$\sqrt{2}$-1,
故答案为:2$\sqrt{2}$-1.
点评 本题考查简单线性规划,涉及向量的模长公式和点到直线的距离公式,准确作图并转化是解决问题的关键,属中档题.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
2.甲乙两人向某个目标射击,他们每次击中目标的概率如下表:
(Ⅰ)若两人同时向目标射击一次,求目标被击中的概率;
(Ⅱ)若由甲开始两人轮流向目标射击,击中目标就停止,现在共有5发子弹,写出使用子弹数?分布列,求?的期望(均值).
| 第一次 | 第二次 | 第三次 | |
| 甲 | 0.4 | 0.6 | 0.8 |
| 乙 | 0.5 | 0.6 | 0.9 |
(Ⅱ)若由甲开始两人轮流向目标射击,击中目标就停止,现在共有5发子弹,写出使用子弹数?分布列,求?的期望(均值).
3.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点分别为F1、F2,过点F1作圆x2+y2=a2的一条切线分别交双曲线的左、右两支于点B、C,与双曲线的渐近线在第二象限内交于点D,且|CD|=|CF2|,则双曲线的离心率为( )
| A. | $\sqrt{6}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
7.若函数$f(x)=lnx+ax+\frac{1}{x}$在[1,+∞)上是单调函数,则a的取值范围是( )
| A. | $(-∞,0]∪[\frac{1}{4},+∞)$ | B. | $(-∞,-\frac{1}{4}]∪[0,+∞)$ | C. | $[-\frac{1}{4},0]$ | D. | (-∞,1] |