题目内容
15.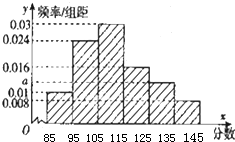 某市在2 015年2月份的高三期末考试中对数学成绩数据统计显示,全市10000名学生的成绩服从正态分布N (120,25),现某校随机抽取了50名学生的数学成绩分析,结果这50名同学的成绩全部介于80分到140分之间现将结果按如下方式分为6组,第一组[85,95),第二组[95,105),…第六组[135,145],得到如图所示的频率分布直方图.
某市在2 015年2月份的高三期末考试中对数学成绩数据统计显示,全市10000名学生的成绩服从正态分布N (120,25),现某校随机抽取了50名学生的数学成绩分析,结果这50名同学的成绩全部介于80分到140分之间现将结果按如下方式分为6组,第一组[85,95),第二组[95,105),…第六组[135,145],得到如图所示的频率分布直方图.(I)试估计该校数学的平均成绩;
(Ⅱ)这50名学生中成绩在125分(含125分)以上的同学中任意抽取3人,该3人在全市前13名的人数记为X,求X的分布列和期望.
附:若 X~N(μ,σ2),则P(u-3σ<X<u+3σ)=0.9974.
分析 (1)根据频率和为1,求出成绩在[120,130)的频率,再计算这组数据的平均数;
(2)根据正态分布的特征,计算50人中成绩在135以上(包括135分)的有50×0.08=4人,而在[125,145)的学生有50×(0.12+0.08)=10,得出X的可能取值,计算对应的概率,列出X的分布列,计算期望值.
解答 解:(1)由频率分布直方图可知[120,130)的频率为1-(0.01×10+0.024×10+0.03×10+0.016×10+0.008×10)=0.12
所以估计该校全体学生的数学平均成绩约为90×0.1+100×0.24+110×0.3+120×0.16+130×0.12+140×0.08=112
(2)由于$\frac{13}{10000}=0.0013$根据正态分布:P(120-3×5<X<120+3×5)=0.9974
故$P(X≥135)=\frac{1-0.9974}{2}=0.0013,即0.0013×10000=13$
所以前13名的成绩全部在135分以上
根据频率分布直方图可知这50人中成绩在135以上(包括135分)的有50×0.08=4人,而在[125,145)的学生有50×(0.12+0.08)=10
所以X的取值为0,1,2,3.
所以P(X=0)=$\frac{{C}_{6}^{3}}{{C}_{10}^{3}}$=$\frac{1}{6}$,
P(X=1)=$\frac{{C}_{6}^{2}{C}_{4}^{1}}{{C}_{10}^{3}}$=$\frac{1}{2}$,
P(X=2)=$\frac{{C}_{6}^{1}{C}_{4}^{2}}{{C}_{10}^{3}}$=$\frac{3}{10}$,
P(X=3)=$\frac{{C}_{4}^{3}}{{C}_{10}^{3}}$=$\frac{1}{30}$;
所以X的分布列为
| X | 0 | 1 | 2 | 3 |
| P | $\frac{1}{6}$ | $\frac{1}{2}$ | $\frac{3}{10}$ | $\frac{1}{30}$ |
点评 本题考查了频率分布直方图的应用问题,也考查了正态分布的应用问题,考查了离散型随机变量的分布列与期望的计算问题,是综合性题目.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | x=0 | B. | x=1 | C. | x=2 | D. | (2,0) |
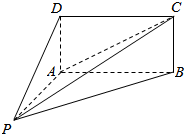 已知如图所示,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
已知如图所示,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.