题目内容
10. 已知如图所示,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
已知如图所示,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.(1)求证:平面PAD⊥平面PAB;
(2)求三棱锥D-PAC的体积;
(3)求直线PC与平面ABCD所成角的正弦值.
分析 (1)由已知条件推导出AB⊥BC,PB⊥BC,由此能证明平面PAD⊥平面PAB.
(2)以A为原点,以平面ABP内过点A作AB的垂线为x轴,AB为y轴,AD为z轴,建立空间直角坐标系,由VD-PAC=VP-ADC,利用等积法能求出三棱锥D-PAC的体积.
(3)求出$\overrightarrow{PC}$和平面ABCD的法向量,由此利用向量法能求出直线PC与平面ABCD所成角的正弦值.
解答 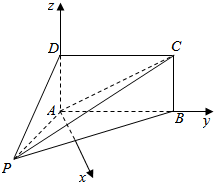 (1)证明:∵四棱锥P-ABCD的底面ABCD为矩形,∴AB⊥BC,
(1)证明:∵四棱锥P-ABCD的底面ABCD为矩形,∴AB⊥BC,
∵∠PBC=90°,∵PB⊥BC,
∵AB∩PB=B,∴BC⊥平面PAB,
∵AD∥BC,∴AD⊥平面PAB,
∵AD?平面PAD,∴平面PAD⊥平面PAB.
(2)解:以A为原点,以平面ABP内过点A作AB的垂线为x轴,AB为y轴,AD为z轴,
建立空间直角坐标系,
由已知得P($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$,0),A(0,0,0),
$\overrightarrow{AP}$=($\frac{\sqrt{3}}{2},-\frac{1}{2},0$),平面ADC的法向量$\overrightarrow{m}$=(1,0,0),
P到平面ADC的距离h=$\frac{|\overrightarrow{AP}•\overrightarrow{m}|}{|\overrightarrow{m}|}$=$\frac{\frac{\sqrt{3}}{2}}{1}$=$\frac{\sqrt{3}}{2}$,
S△ADC=$\frac{1}{2}×2×1$=1,
∴三棱锥D-PAC的体积:
VD-PAC=VP-ADC=$\frac{1}{3}×h×{S}_{△ADC}$=$\frac{1}{3}×\frac{\sqrt{3}}{2}×1$=$\frac{\sqrt{3}}{6}$.
(3)解:P($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$,0),C(0,2,1),$\overrightarrow{PC}$=(-$\frac{\sqrt{3}}{2}$,$\frac{5}{2}$,1),
平面ABCD的法向量$\overrightarrow{m}$=(1,0,0),
设直线PC与平面ABCD所成角的为θ,
则sinθ=|cos<$\overrightarrow{m}$,$\overrightarrow{PC}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{PC}}{|\overrightarrow{m}|•|\overrightarrow{PC}|}$|=|$\frac{-\frac{\sqrt{3}}{2}}{\sqrt{\frac{3}{4}+\frac{25}{4}+1}}$|=$\frac{\sqrt{6}}{8}$.
∴直线PC与平面ABCD所成角的正弦值为$\frac{\sqrt{6}}{8}$.
点评 本题考查面面垂直的证明,考查三棱锥的体积的求法,考查直线与平面所成角的正弦值的求法,是中档题,解题时要注意空间思维能力的培养.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案| A. | {1} | B. | {3} | C. | {1,3} | D. | {1,2,3} |
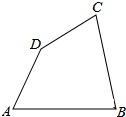 如图,凸四边形ABCD,求作一个三角形,使得该三角形的面积和凸四边形ABCD的面积相等.
如图,凸四边形ABCD,求作一个三角形,使得该三角形的面积和凸四边形ABCD的面积相等. 某市在2 015年2月份的高三期末考试中对数学成绩数据统计显示,全市10000名学生的成绩服从正态分布N (120,25),现某校随机抽取了50名学生的数学成绩分析,结果这50名同学的成绩全部介于80分到140分之间现将结果按如下方式分为6组,第一组[85,95),第二组[95,105),…第六组[135,145],得到如图所示的频率分布直方图.
某市在2 015年2月份的高三期末考试中对数学成绩数据统计显示,全市10000名学生的成绩服从正态分布N (120,25),现某校随机抽取了50名学生的数学成绩分析,结果这50名同学的成绩全部介于80分到140分之间现将结果按如下方式分为6组,第一组[85,95),第二组[95,105),…第六组[135,145],得到如图所示的频率分布直方图.